本文转自知乎专栏 信口开河
矩阵的特征向量跟特征值的英文名字分别是 eigenvector 跟 eigenvalue,这俩概念非常非常有用,根据他们俩可以外延出很多有趣的功能。大部分同学可能脑子里想一下还能记得他们俩是怎么计算出来的,但是他们为什么可以代表一个矩阵的“特征”呢?除了这俩,相信大多数同学都不记得矩阵的行列式是个什么东西了,总之不太直观。相比较而言,矩阵的迹(trace)这个概念就比较直观,就是主对角线上的元素之和。本篇文章主要围绕这四个概念,讲一下这四个东西是如何刻画矩阵的特征跟他们之间的关联。
“eigen”在德语里的意思是“自身的”,“固有的”,在我们汉语里把它翻译成“特征”;无论德语还是汉语,都表达出了特征值跟特征向量其实是一个矩阵内在的,独有的东西。特征值跟特征向量是定义在方阵上的,为了方便通过图表描述,我们从最简单的2*2方阵入手:把方阵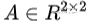 理解成二维平面上的一个映射,平面上任意一个向量
理解成二维平面上的一个映射,平面上任意一个向量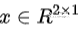 都可以被映射成一个新的向量
都可以被映射成一个新的向量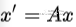 ,画在图上就是
,画在图上就是

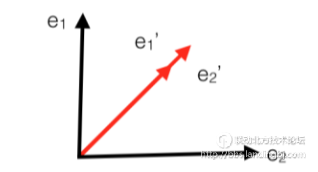
对比着俩图可以发现,对于一个固定的矩阵A,一般的向量被他transform之后都会改变方向,但是有一些特殊的向量,被A映射了之后还是保持它本来的方向,改变的只是它的模长。这些特殊向量的方向不变性表达出来就是这样的:
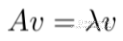
等式的右边,v表示向量原本的方向,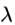 表示向量模长的变化。特征向量的定义就是这些特殊的向量。那么特征向量究竟有什么好处呢?假设现在有个场景,我们需要把一个向量给transform 100次,也就是计算一下
表示向量模长的变化。特征向量的定义就是这些特殊的向量。那么特征向量究竟有什么好处呢?假设现在有个场景,我们需要把一个向量给transform 100次,也就是计算一下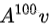 。最简单粗暴的办法是直接计算100次矩阵乘法;稍微聪明一点的方法是先计算序列
。最简单粗暴的办法是直接计算100次矩阵乘法;稍微聪明一点的方法是先计算序列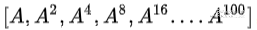 ,这样只要十几次次矩阵乘法就能搞定;不过最方便的还是要从特征值跟特征向量入手。假设v是A的特征向量,并且能满足上面这个式子,于是有
,这样只要十几次次矩阵乘法就能搞定;不过最方便的还是要从特征值跟特征向量入手。假设v是A的特征向量,并且能满足上面这个式子,于是有
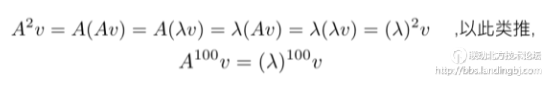
可以发现如果v是特征向量,就不需要计算任何矩阵乘法了,只需要计算十几次乘法就行了。其实对于任意向量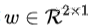 ,我们仍然可以从特征向量入手,w可以由A的特征向量线性组成而成:
,我们仍然可以从特征向量入手,w可以由A的特征向量线性组成而成:
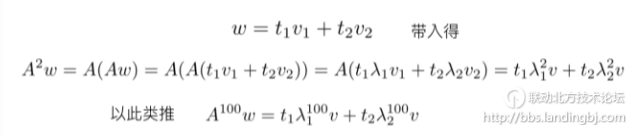
这样来看,特征向量会大幅简化某些矩阵运算,那么要如何计算特征向量呢?从特征向量的定义出发:
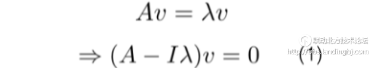
从这个方程里,我们不但需要得到v,也需要得到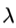 。把原问题转化成方程(1)之后,可以发现方程(1)没有常数项,以二维为例可以把(1)写成:
。把原问题转化成方程(1)之后,可以发现方程(1)没有常数项,以二维为例可以把(1)写成:
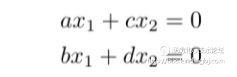
这个方程组想要有非零解,必须得满足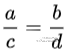 也就是 (a,c) 跟 (b,d) 共线。也就是教科书上说的矩阵A不满秩(p.s. 方阵的秩定义为矩阵中线性不相关的行跟列的个数)。教科书上还告诉我们不满秩的充要条件是矩阵的行列式等于零。矩阵的秩的概念比较容易理解,行列式却没有这么直观。其实 determinant 这个单词被翻译为行列式个人认为不是很传神,感觉 determinant 也需要一个带点“特征”含义的中文名。
也就是 (a,c) 跟 (b,d) 共线。也就是教科书上说的矩阵A不满秩(p.s. 方阵的秩定义为矩阵中线性不相关的行跟列的个数)。教科书上还告诉我们不满秩的充要条件是矩阵的行列式等于零。矩阵的秩的概念比较容易理解,行列式却没有这么直观。其实 determinant 这个单词被翻译为行列式个人认为不是很传神,感觉 determinant 也需要一个带点“特征”含义的中文名。
与矩阵的秩相似,行列式也是一个数值。还是把矩阵当成一个映射,那么 (0, 1) 跟 (1, 0) 这对基可以被映射成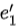 ,
,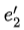 ,如图所示,那么矩阵A的行列式就被定义为由
,如图所示,那么矩阵A的行列式就被定义为由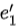 ,
,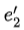 这两个向量延伸出来的平行四边形的面积:
这两个向量延伸出来的平行四边形的面积:
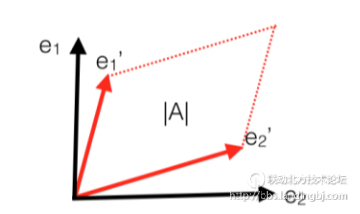
用这种方式让一个矩阵跟一个数值产生关系简直是神来之笔。更神奇的是这样做,特征值,特征向量,行列式就关联起来了。不满秩要求行列式为零,那么什么时候一个平行四边形的面积会变成0呢?可以发现,当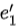 ,
,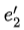 这俩向量平行的时候,就没什么平行四边形了,平面上就只剩下了一条线段:
这俩向量平行的时候,就没什么平行四边形了,平面上就只剩下了一条线段:
什么样的矩阵会产生这种效果呢?对于二维矩阵来说,只要它的两个行向量共线就可以。重新理一下我们现在的逻辑线条:想让方程组(1)有非零解,必须让它的行向量共线,想让行向量共线,只需要A的行列式为零;二维矩阵的行列式等于平行四边形的面积,三维矩阵的行列式对应的是平行六面体的体积....更高维度上也可以延伸出同样的类似于“体积”的定义。
那么面积要怎么算呢?还是以二维平面为例,两个向量构成的平行四边形的面积可以由下面这个公式计算 (粉红的图片来自维基百科)
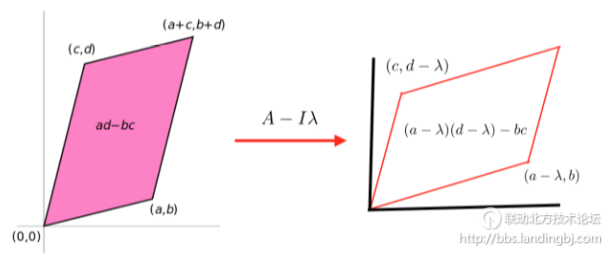
令这个计算面积的公式等于零:
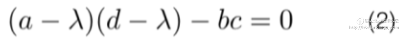
这个方程就是课本上的特征方程,方程的解就是特征值。特征方程的解也可以写成这种形式:
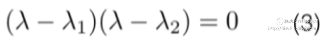
方程(2)跟方程(3)必须是一回事。观察一下这俩方程,可以发现(2)的常数项是 ad-bc; 方程(3)的常数项是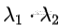 。结合前面讲的矩阵A的行列式(平行四边形的面积)可以发现:
。结合前面讲的矩阵A的行列式(平行四边形的面积)可以发现: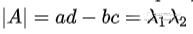 ;对,这不是巧合,实际上在任意维度的矩阵上同样可以证明
;对,这不是巧合,实际上在任意维度的矩阵上同样可以证明
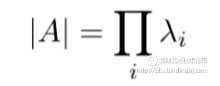
也就是行列式等于特征值的乘积。
到此为止,这哥三通过各种神来之笔被联系在了一起,下面我们再来分析下两种特殊的矩阵对应的这三个值。让我们回去看看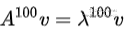 ,在这个式子中,如果
,在这个式子中,如果 ,那么经过多次迭代,
,那么经过多次迭代, 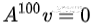 ;如果
;如果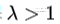 , 那么
, 那么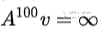 。于是,当且仅当
。于是,当且仅当 的时候经过多次迭代,还能剩下一个稳定的向量。这个性质是不是有点似曾相识?没错,马尔科夫链的概率转移矩阵就是这样的矩阵。在马尔科夫链中,经过足够多次跳转之后,状态分布趋向一个稳定的值。马尔科夫链的概率转矩阵需要满足的条件是:每一行都满足行元素之和为1。相反方向也同样成立:如果一个矩阵满足每一行的元素之和都是1,那么它必定有一个为1的特征值。
的时候经过多次迭代,还能剩下一个稳定的向量。这个性质是不是有点似曾相识?没错,马尔科夫链的概率转移矩阵就是这样的矩阵。在马尔科夫链中,经过足够多次跳转之后,状态分布趋向一个稳定的值。马尔科夫链的概率转矩阵需要满足的条件是:每一行都满足行元素之和为1。相反方向也同样成立:如果一个矩阵满足每一行的元素之和都是1,那么它必定有一个为1的特征值。
除了马尔科夫概率转移矩阵,还有一种矩阵的特征向量有特殊的性质:对称矩阵的特征向量相互之间正交。证明如下,对于任意两个向量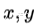 跟矩阵 A, 有
跟矩阵 A, 有
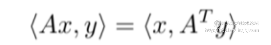
如果A是一个对称矩阵,并且x,y分别是A的两个不同的特征向量对应的特征值分别为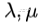 ,那么便有
,那么便有
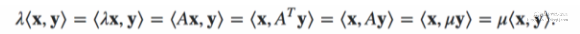
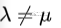 为了让上式满足,只有令
为了让上式满足,只有令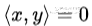 即特征向量之间两两正交。这个性质非常非常有用,在我们的降维系列里面会常常用到。
即特征向量之间两两正交。这个性质非常非常有用,在我们的降维系列里面会常常用到。
最后轮到矩阵的trace了,个人觉得trace的中文翻译就更渣了,居然就直勾勾的叫作迹。。。trace的英文名字感觉还跟它的物理意义挺搭的:拿到一个矩阵,我们沿着主对角线往下走到最后,所有元素的和就是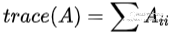
下面,高能的部分来了: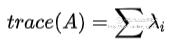 ,矩阵的trace等于特征值之和,也就是说矩阵的主对角线元素之和等于它的特征值之和。对于这个性质作者暂时也还没能想到一个直观的解释,证明的思路跟证明前面的那个行列式等于特征值之和类似,要从特征方程的表达式入手.
,矩阵的trace等于特征值之和,也就是说矩阵的主对角线元素之和等于它的特征值之和。对于这个性质作者暂时也还没能想到一个直观的解释,证明的思路跟证明前面的那个行列式等于特征值之和类似,要从特征方程的表达式入手.


 技术讨论
技术讨论