转自公众号机器学习和数据挖掘
昨天有朋友问PCA算法的一些细节问题,今天就写一篇PCA的文章,主要讲述PCA的整个过程以及其中的一些细节问题。
一、PCA过程
1、计算每一个维度的平均值,然后对每一个样本取值减去其对应维度的平均值,一般情况下还应该进行归一化。如下图:
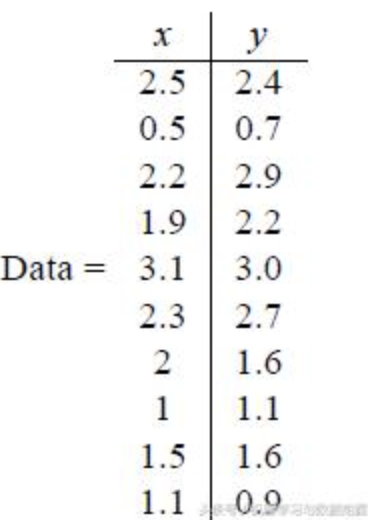
原始数据
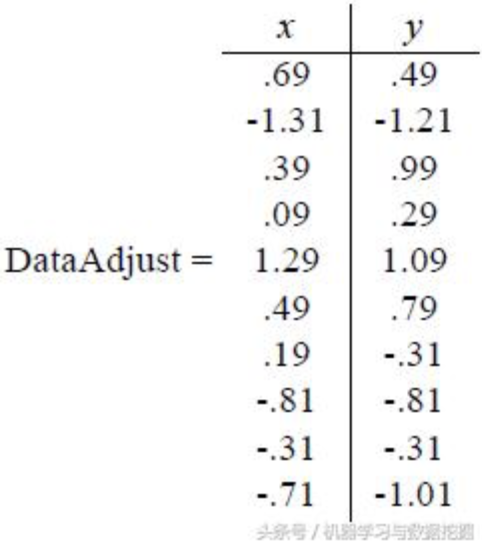
减去均值后的数据
2、求特征协方差矩阵
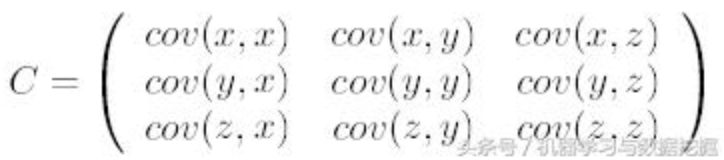
对于一个3维数据对应的协方差矩阵
3、协方差的特征值和特征向量
4、将特征值按照从大到小的顺序排序,选择其中最大的k个(降维到K维),然后将其对应的k个特征向量分别作为列向量组成特征向量矩阵。
5、将原始样本数据投影到选取的特征向量上。
比如:假设样本数为m,特征数为n,减去均值后的样本矩阵为DataAdjust(m*n),协方差矩阵是n*n,选取的k个特征向量组成的矩阵为EigenVectors(n*k)。那么投影后的数据FinalData为
那么,问题就来了,为什么协方差矩阵前K个特征值对应的方差就是最大的呢?,这就是方差最大理论了。
二、PCA理论基础
在信号处理中认为信号具有较大的方差,噪声有较小的方差,信噪比就是信号与噪声的方差比,越大越好。赝本在那个维度的的投影方差较小,那么认为那个维度的投影是由噪声引起的。因此我们认为,最好的k维特征是将n维样本点转换为k维后,每一维上的样本方差都很大。
比如下图有5个样本点:(已经做过预处理,均值为0,特征方差归一)
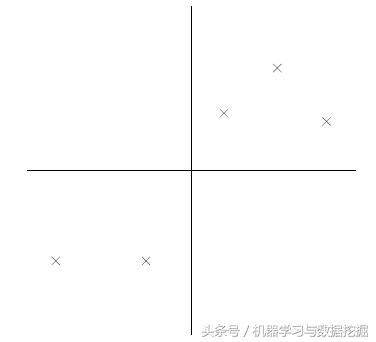
下面将样本投影到某一维上,这里用一条过原点的直线表示(前处理的过程实质是将原点移到样本点的中心点)。
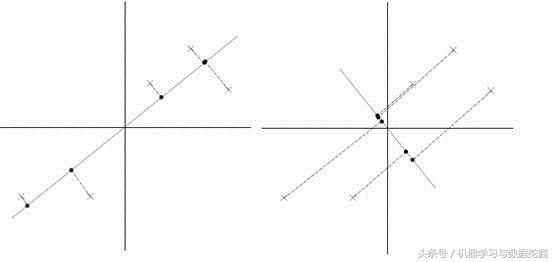
假设我们选择两条不同的直线做投影,那么左右两条中哪个好呢?根据我们之前的方差最大化理论,左边的好,因为投影后的样本点之间方差大一些。
关于样本点投影的概念,通过下图可以明白。
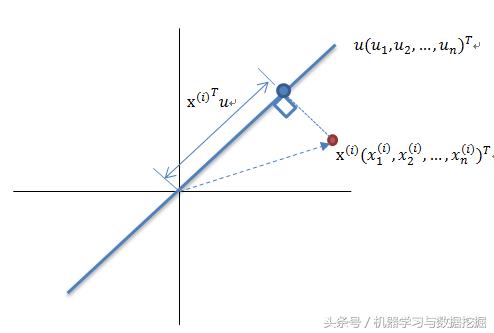
u是一个单位向量,也就是说u向量决定我的样本按照哪个方向映射,这时候方差才大。
由于原始数据已经是0均值的了,因此经过映射之后也是0均值的
我们只需要对协方差矩阵进行特征值分解,得到的前k大特征值对应的特征向量就是最佳的k维新特征,而且这k维新特征是正交的。得到前k个u以后,样例xi通过以下变换可以得到新的样本。
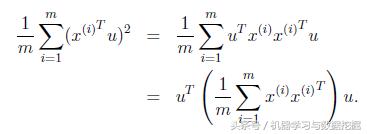
中间那部分很熟悉啊,不就是样本特征的协方差矩阵么xi的均值为0,上式可以改写为
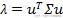
由于u是单位向量,即
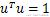
上式两边都左乘u得,
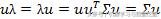
即
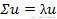
这不就是说明方差最大的方向就是按前K个特征值对应的特征向量映射的方向吗。
该贴被huang.wang编辑于2018-10-19 11:44:05


 技术讨论
技术讨论