超图的基本概念
在传统的图理论研究中,研究者往往假设数据对象之间的关系是两两对应的序对关系。这种简单的假设便于数据通过常见的普通图来进行表示。在普通图里,一个数据对象表示一个顶点,两个顶点之间的边用来描绘顶点之间的序列关系。在现实生活中,数据对象之间的关系既可能是对称的也可能是非对称的。举个简单的例子,两幢建筑物的距离关系就是典型的对称关系,我们可以说A建筑物到B建筑物的距离是100米,同时我们也可以说B建筑物到A建筑物的距离是100米。与前面的例子相反,师生关系是一个典型的非对称关系。我们可以说A是B的老师却不能说B是A的老师。幸运的是,图学习方法能够分别通过构建无向图和有向图来描述对称和非对称关系。对于计算机视觉和图像处理问题,对称的数据对象关系比较常见。
在现实世界中,数据对象之间关系不会只是简单的单对单的序列关系,大多数关系都是一对多甚至多对多的复杂多元关系。比如,在分类问题中,类和样本之间的关系往往一对多的。而在属性学习的问题中,样本和属性之间的关系则是多对多的。普通图显然不能直观地、合理地描述这些复杂的多元关系,从而限制了图理论在计算机视觉领域的应用。20世纪末21世纪初,随着图学习的算法在计算机视觉领域的流行,超图技术也逐渐被引入计算机视觉领域[84][85]。超图与图的主要区别是图中边上的顶点数目不同。普通图的边只有两个顶点,而超图的可以具有任意多个顶点。为了和普通图的边进行区分,超图的边也称为超边。下面将简单地介绍超图的一些基本定义。
给定一个超图G=(V,E,w),V是一个有限的顶点集,E是超图的超边集。任意一个超边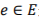 是顶点集V的一个子集,
是顶点集V的一个子集,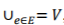 ,并被赋予一个非负权重
,并被赋予一个非负权重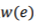 。
。
对于任意顶点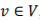 ,它的阶(或称为度,Degree)可被定义为如下表达式:
,它的阶(或称为度,Degree)可被定义为如下表达式:
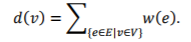
对于超边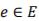 ,它的阶可以定义为边上所有顶点的数目
,它的阶可以定义为边上所有顶点的数目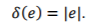
方阵Dv、De、W分别定义为顶点阶、超边阶和超边权重的对角矩阵。超图的结构可以通过一个 维的点边关联矩阵H来进行描述。在该矩阵中,如果一个顶点e在一个超边V上,其第(v,e)个元素被赋值为1,h(v,e)=1,如果该顶点不在该边上,则设置相关元素的值为0。根据关联矩阵的定义,上文梁公视可以进一步表达为
维的点边关联矩阵H来进行描述。在该矩阵中,如果一个顶点e在一个超边V上,其第(v,e)个元素被赋值为1,h(v,e)=1,如果该顶点不在该边上,则设置相关元素的值为0。根据关联矩阵的定义,上文梁公视可以进一步表达为
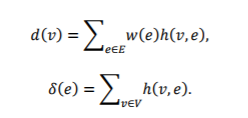
很多超图算法可以归纳为一个超图分割(Hypergraph Partition)问题。对于一个超图G=(V,E,w),一条超图切(Hypergraph Cut)把超图的顶点集分割成两个子集,一个是顶点子集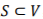 ,一个是它补集为Sc。超边可以被认为是一条同时与顶点子集和都关联的超图切。对于顶点子集,可以定义一个超边集(HypergraphSet)作为它的超边边界(Hyperedge Boundary):
,一个是它补集为Sc。超边可以被认为是一条同时与顶点子集和都关联的超图切。对于顶点子集,可以定义一个超边集(HypergraphSet)作为它的超边边界(Hyperedge Boundary):
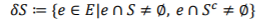
这个超边集就是把超图分割成的S和Sc两个子集的割集。我们定义子集S的体积volS为该顶点集中顶点阶之和:
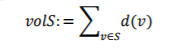
定义该顶点子集的超边边界的体积volS为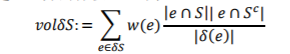
根据式以上公式,不难推测出顶点子集的超边边界体积和其补集的超边边界体积是相等的,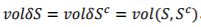 。根据以上公式以及定义,可以把超边边界的体积理解为顶点子集和它的补集的之间连接紧密度,把顶点子集的体积视作两个顶点子集内部的连接紧密度。在超图分割问题中,我们试图学习一个超图切(Hypergraph Cut)。它能够将顶点集分割成两个子集,这些子集之间的连接程度应该是稀疏的,而这些顶点子集内部的连接应该紧密的。上述超图分割问题可以被转化为以下优化问题:
。根据以上公式以及定义,可以把超边边界的体积理解为顶点子集和它的补集的之间连接紧密度,把顶点子集的体积视作两个顶点子集内部的连接紧密度。在超图分割问题中,我们试图学习一个超图切(Hypergraph Cut)。它能够将顶点集分割成两个子集,这些子集之间的连接程度应该是稀疏的,而这些顶点子集内部的连接应该紧密的。上述超图分割问题可以被转化为以下优化问题:
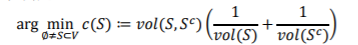
其中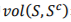 表示两个顶点子集之间的超边边界体积而表示顶点子集的体积。对于普通图的情况
表示两个顶点子集之间的超边边界体积而表示顶点子集的体积。对于普通图的情况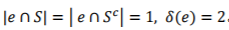 。上式也可以被归纳为一个归一化分割(NormalizedCut,简称Ncut)模型乘以标量1/2。
。上式也可以被归纳为一个归一化分割(NormalizedCut,简称Ncut)模型乘以标量1/2。
常见超图算法
度量多点之间的关系在数学领域并不算一个新的概念。然而,直到80年代末90年代初,超图理论才陆续被引入计算机领域。最初的超图理论主要是被用于解决VLSI电路分割问题。90年代末超图技术才逐步应用到计算机视觉、机器学习、模式识别、图像处理等领域。根据综述文献,超图学习方法主要可以分为三大类。第一类的方法是在原来超图基础上构建一个普通图,然后利用基于普通图的谱聚类的方法对超图进行分割。这类方法的代表算法包括团扩张(Clique Expansion)、星形扩张(Star Expansion)、罗德里格斯拉普拉斯(Rodriquez’sLaplacian)以及团平均(Clique Averaging)等算法。团扩张和星形扩张是最常见的两个利用普通图对超图进行近似的方法。在团扩张算法中,每条超边都被视作普通图的一个子团(Clique)。星形扩张通过对每条超边给定一个伪顶点并连接该伪顶点与超边上所有其他顶点的方式来构建一个普通图用以近似表达超图结构。团平均和团扩张算法非常相似,但它能保留更多原超图的信息。第二类方法是通过利用普通图拉普拉斯(Graph Laplacian)模拟描述一个超图拉普拉斯(Hypergraph Laplacian)。这类方法的代表性方法主要有周氏标准化拉普拉斯(Zhou’sNormalized Laplacian)和博拉拉普拉斯(Bolla Laplacian)等方法。根据文献的研究,前两类算法在特定情况下其实是相互等价的。第三类方法是基于张量的超图学习方法。在该类方法中,超图结构被张量所描述,然后利用联合聚类的方法对超图进行分割。这类的方法主要的缺点是要求超边的大小一致而且对计算机复杂度和内存需求要求比较高。本文将会详细介绍前面提到的几类常见的超图学习算法。在本节将会着重介绍周氏标准化拉普拉斯算法,因为它为本文的研究内容奠定了理论基础。
1、星形扩张算法
星形扩张(Star Expansion)算法通过对每一条超边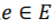 引入一个新的顶点并把该顶点和对应超边上所有顶点相连接,从而能够从原来的超图
引入一个新的顶点并把该顶点和对应超边上所有顶点相连接,从而能够从原来的超图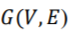 中构建出一个新的普通图)。其中,
中构建出一个新的普通图)。其中,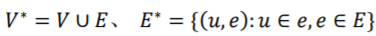 。这样每条超边都对应新构建的普通图中的一个星形结构且这个新构建的普通图是个双向图。在星形扩张方法中,新构建的普通图的边权重可以通过以下方式从原来超图的边权重推算出。
。这样每条超边都对应新构建的普通图中的一个星形结构且这个新构建的普通图是个双向图。在星形扩张方法中,新构建的普通图的边权重可以通过以下方式从原来超图的边权重推算出。
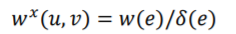
这样就可以利用学习到的普通图拉普拉斯对原来的超图进行分割。
2、团扩张算法
团扩张(Clique Expansion)算法把每条超边视作一个全联通的子图(可以称为团,Clique)。这样一个超边可以被其所含的任意两个顶点之间边的集合所表示,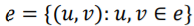 。从而超图
。从而超图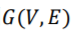 就可以转化为一个普通图
就可以转化为一个普通图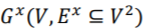 。对于图
。对于图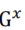 中的边,其最优权重
中的边,其最优权重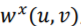 应该最小化该权重与涵盖它的超边的权重的差值:
应该最小化该权重与涵盖它的超边的权重的差值:
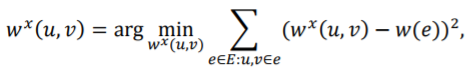
上式的解为:
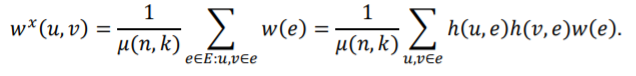
其中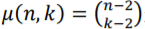 是该超边两点普通边的数目,是所有顶点的数目而是超边所含顶点的数目。在团扩张算法中,超边中两点的权重赋值比较简单,它假设同一条超边中任意两点普通边的权重都是相等的。
是该超边两点普通边的数目,是所有顶点的数目而是超边所含顶点的数目。在团扩张算法中,超边中两点的权重赋值比较简单,它假设同一条超边中任意两点普通边的权重都是相等的。
3、团平均算法
团平均(Clique Averaging)算法通常被用来解决利用普通图来描述超图结构的问题。团平均算法和团扩张算法非常相似。在该算法中,超边的权重和对应普通图的边权重的关系定义如下:
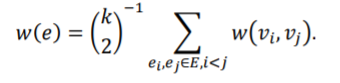
由上式可知,团的权重和超边的权重是成正比的。假设超边集中超边根据超边上顶点的下标进行有序排列同时对应的简单图的边也是按照这种准则排列,我们可以定义一个0-1关联矩阵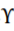 用来根据顶点的下标来描绘原超图中超边与新构建普通图的边之间的关联
用来根据顶点的下标来描绘原超图中超边与新构建普通图的边之间的关联

定义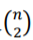 维向量d2为简单图边权重向量,dk为超图的超边权重向量。那么上面式子可以写成以下矩阵形式:
维向量d2为简单图边权重向量,dk为超图的超边权重向量。那么上面式子可以写成以下矩阵形式:
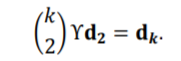
因为权重是非负的,所以假设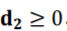 。如果强制对d2加一个上界,
。如果强制对d2加一个上界,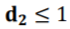 ,以上用普通图近似描述超图的问题可以转化为寻找一个满足以下目标的边权重向量d2的问题:
,以上用普通图近似描述超图的问题可以转化为寻找一个满足以下目标的边权重向量d2的问题:
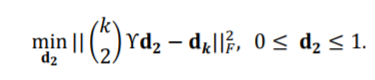
实质上,该问题和前一小节介绍的团扩张问题非常近似。如果定义团扩张问题中的超边e所对应团的边权重向量为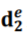 ,那么式上文式子其实可以进一步推导成以下形式:
,那么式上文式子其实可以进一步推导成以下形式:
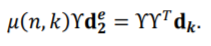
可以发现它们的区别仅上文式子的右项多乘了一个矩阵。由于这是一个非负对称阵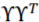 ,所以其实相当于只是对超边权重做了一次二次方的卷积。由于
,所以其实相当于只是对超边权重做了一次二次方的卷积。由于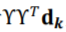 只是
只是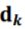 的低通版本,所以团扩张所学习出的近似普通图和团平均算法所学习出的近似普通图是十分相似的,后者只是前者的一个低通版本。虽然团扩张和团平均模型在数学表达上有着明显区别,但从性能上看,其实它们的表现比较类似。
的低通版本,所以团扩张所学习出的近似普通图和团平均算法所学习出的近似普通图是十分相似的,后者只是前者的一个低通版本。虽然团扩张和团平均模型在数学表达上有着明显区别,但从性能上看,其实它们的表现比较类似。
4、博拉拉普拉斯
博拉等人利用顶点阶的对角矩阵Dv、边阶的对角矩阵De和关联矩阵H对一个无权重的超图定义了其拉普拉斯矩阵:
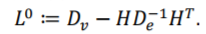
根据文献,博拉拉普拉斯的特征向量定义了该无权重超图的“最好”欧式嵌入(The‘Best’Euclidean Embedding)。
5、罗德里格斯拉普拉斯
从无权重超图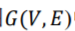 中构建出了一个普通图
中构建出了一个普通图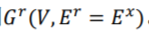 。与团扩张算法相同,罗德里格斯拉普拉斯算法也把超图中的超边视作普通图中的团(Clique)。在该普通图中,一条连接顶点和的普通边的权重是包含它的超边的数目:
。与团扩张算法相同,罗德里格斯拉普拉斯算法也把超图中的超边视作普通图中的团(Clique)。在该普通图中,一条连接顶点和的普通边的权重是包含它的超边的数目:
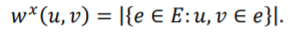
该新构建的普通图就可以通过以下方式来描述原超图的结构:
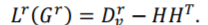
其中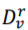 表示普通图
表示普通图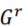 的顶点度数矩阵。与博拉拉普拉斯算法相同,罗德里格斯拉普拉斯算法也是用来描绘一个无权重超图的结构的算法,所以它们都具有类似的几何性质。
的顶点度数矩阵。与博拉拉普拉斯算法相同,罗德里格斯拉普拉斯算法也是用来描绘一个无权重超图的结构的算法,所以它们都具有类似的几何性质。
6、吉布森动力系统
吉布森动力系统(Gibson’sDynamical System)是一种对数据进行聚类的动力系统。这个动力系统也利用超图来描述数据关系。它的求解过程可以归纳为以重庆大学博士学位论文20下简单的迭代过程:
1)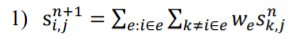
2)正交并归一化向量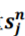 。
。
该迭代过程实质上是计算邻接矩阵,,特征向量的幂方法。
7、李氏邻接矩阵法
李氏邻接矩阵算法(Li’s Adjacency Matrix)首先定义了一个与星形扩张类似的单一无权重超图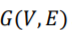 。然后,该方法直接定义
。然后,该方法直接定义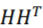 为一个描述超图结构的
为一个描述超图结构的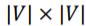 维邻接矩阵。最后,该方法验证了新构建的连接矩阵和原来超图具有相似的谱特性。
维邻接矩阵。最后,该方法验证了新构建的连接矩阵和原来超图具有相似的谱特性。
8、各超图算法之间联系
许多超图算法在一些特定条件下实质是相互等价的。
该贴被huang.wang编辑于2018-9-30 17:02:44


 技术讨论
技术讨论