近年来随着复杂网络研究的不断深入,复杂网络理论及应用得到了前所未有的蓬勃发展。然而现实世界中的许多网络是复杂多变的,网络规模在不断扩大,节点间的关系也不仅仅局限二维关系上。超网络概念的提出为描述和解决这一类问题提供了新思路。虽然对超网络本身还没有公认的定义,对什么样的网络可以算作超网络也还有一个逐步明确的过程,但研究者已经逐步找到了它的一些特征,并在此基础上建立了一些模型,提出了合适的描述方法。从现有的研究成果来看,关于超网络理论的研究成果主要在以下几个方面:
超网络的定义
近年来对于超网络的定义主要从一下两个角度进行:
1、基于网络结构形成理论的超网络定义
2006 年,Frank.H 在经济学领域将超网络描述为“网络中的网络”,他提出超网络中各个有向网络作为节点,网络的结合偏好和网络形成的管理规则作为连接节点的边,而超网络唯一地表示了由这些规则支配的所有结合移动和结合偏好(这些规则支配了超网络边之间的加、减或替换)。这种基于网络结构形成理论提出的超网络定义已经被广泛运用于社会网络、知识网络等领域的复杂网络系统研究中。
2、基于超图理论的超网络定义
超图(Hypergraph)是图论的分支,是有限集合的子集系统,是最一般的离散结构,在信息科学、生命科学等领域有着广泛的应用。超图的概念最早于 1970 年由法国数学家 Berge提出,他系统地建立了无向超图理论,并应用拟阵结构来研究超图理论在运筹学方面的应用。定义:
设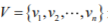 是一个有限集。若
是一个有限集。若
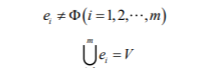
则称二元关系, H=(V,E)是一个超图。V的元素v1,v2,...vn称为超图的顶点,E={e1,e2,...,en}是超图的超边集合,集合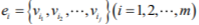 称为超边。
称为超边。
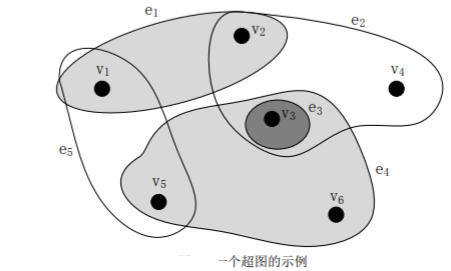
如上图所示,V={v1,v2,...v6}是超图的顶点集,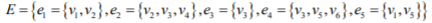 是超图的超边集。
是超图的超边集。
以此为基础,Estrada 和 Rodriguez 提出把具有超图拓扑结构的网络称为超网络(Hypernetwork)。基于超图的超网络动态演化模型能够很好地描述和表示超网络中各节点100 之间的相互作用和影响,但只有对实际超网络的结构特征有很好的了解,才能建立合适的基于超图的超网络模型。
基于超图的超网络理论研究现状
超网络理论的研究以超图理论为基础。研究者将复杂网络研究中的平均路径长度、集聚系数、度分布、介数等网络度量拓展至超图领域,并在此基础上引入 k-超树、超回路、超通路、超边分解等概念,并在此基础上建立了有向超图。应用超图理论,Estrada 105等对于复杂超网络的子图中心度和集聚系数进行了研究,从理论上给出了超网络的子图中心度和集聚系数的定义及公式,并对三个真实的复杂系统的子图中心度和集聚系数在一般复杂网络和超网络之间的不同做了比较。该文献的研究结果可作为进一步研究超网络的无标度特性、小世界特性及可靠性等性质的研究基础。Ghoshal等针对随机三部超图及其应用展开了系统研究,并根据大众分类网络的资源、用户、标签之间的关系构建了符合实际的随机超网络,并利用普通随机图的计算方法计算了随机超图的一些性质,得到了一些重要结果。Zlatic等基于三部超图模型的统计特性,定义和分析和超网络的几个拓扑量:超度的分布、顶点的相似性、超网络的聚集性、定点之间的距离以及超网络的社团结构进行了定义,并用这些拓扑量对真实超网络进行了仿真分析。张子柯等建立了一种基于用户背景知识和对象、标签双115 重优先连接机制的超网络增长模型,在此超网络模型上分析超度、集聚系数及平均路径长度等特性。Johnson 等分析了图、超图、网络、单纯复形、复用网络及超网络之间的关系,着重分析了在网络科学中的 n 元关系。Daniele的研究提供了寻找 s-超网络的一个简单而快速的算法,并证明此多项式可解类是线性时间内可解的。
超网络的演化模型研究现状
120 王建伟等给出了一种基于超图的超网络动态演化模型。在他们的模型中采用了增长和超度优先链接机制,每次新增加若干节点和超网络中已有的一个节点结合生成超边。裴伟东等研究了基于一类三角形结构的动态超网络结构的演化模型,通过平均场方法理论分析超网络特性,发现该类演化模型具有无标度和小世界现象。胡枫等参考 BA 无标度网络的构建方法,即每次增加一个新节点和超网络中已存在的 m 个旧节点组合生成超边,构建了 型均匀超网络模型。对比 BA 无标度网络生成的两大机制:节点增长和节点度优先,在超网络中采取超边增长和超度优先机制,每次新增加的节点与原超网络中节点结合的概率与超网络节点超度成正比,保证了超网络的无标度特性。
结合王和胡的工作,祝昕昀等构建了更具普遍性的(m1+m2)型均匀超网络模型(其中m1表示新增节点数量,m2表示与新节点形成超边的老节点数量),并利用Poisson 过程130 理论和连续化方法对模型进行分析,获得网络稳态平均超度分布的解析表达式。分析结果表明这个超网络的稳态平均超度是与到达过程无关的幂律分布,但这个稳态平均超度分布指数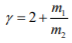 与超边内节点数有关。如果m1>m2,幂律指数表现的比较大,超网络的超度分布有趋向于指数分布的趋势,这正是超网络演化与普通复杂网络演化的不同之处。郭进利将问题拓展至更为普遍的情况,建立非线性择优连接非均齐超网络演化模型,并研究其演化机制和拓扑性质。结果表明这类超网络的稳态平均超度分布是渐近时间无关的,尽管网络持续增长,但超网络节点平均超度分布达到一个稳定的状态表现出拉直指数分布。
与超边内节点数有关。如果m1>m2,幂律指数表现的比较大,超网络的超度分布有趋向于指数分布的趋势,这正是超网络演化与普通复杂网络演化的不同之处。郭进利将问题拓展至更为普遍的情况,建立非线性择优连接非均齐超网络演化模型,并研究其演化机制和拓扑性质。结果表明这类超网络的稳态平均超度分布是渐近时间无关的,尽管网络持续增长,但超网络节点平均超度分布达到一个稳定的状态表现出拉直指数分布。
超网络理论研究存在的问题
超网络概念的提出使得人们对一些多层、多级、多维网络流及多属性、多准则的网络问题有了新的认识,但目前对超网络的研究还处于逐步明确的状态,尚无公认的定义和完整的理论体系。因此对超网络理论及动力学行为的研究仍处于相对匮乏的状态。
现有研究已经将复杂网络的子中心度、集聚系数等参数及研究方法推广到了超网络,但对于真实世界的各类超网络,这些特征量还不能描述一个复杂超网络的全部特征。而且现有研究表明超网络的一些特性与一般复杂网络的对应特征有所不同,研究者还在不断寻找其他特征量来描述超网络的各种特征,例如描述网络模块结构的模块特征(社区特征)、描述网络等级结构的等级特征、描述超网络超边权重的特征等。如何将一般复杂网络的拓扑特征研究拓展到超网络中,并寻找和发现能够更全面描述超网络拓扑特征的特征量仍然是重要的研究内容。此外,基于 BA 模型的超网络演化模型研究大多建立在均匀超网络的基础上(即每一条超边包含的节点数相同),并不具有普遍性意义。而且目前针对超网络鲁棒性和脆弱性的研究相对匮乏,对于干扰情况或网络结构遭到破坏情况下超网络的稳定性了解甚少。
该贴被huang.wang编辑于2018-9-28 17:53:02


 技术讨论
技术讨论