本文转自头条 超级数学建模

爱因斯坦和波尔的世纪论战燃爆了整个20世纪初的物理学界。

争论促进了物理学的发展，吸引了更多人的关注，很多的学者和吃瓜群众更是对争论乐此不疲，津津乐道，就像是看一部跌但起伏的武侠小说，对各大门派的英雄以及他们的看家本领如数家珍。

同样，作为一项基础研究的统计学，也不乏著名的论战和门派之争。下面我们就复盘一下统计学上的一出著名的门派之争，直到现在双方都难分高下。

统计学的研究目的就是要通过获取的已有数据对系统未知的知识做出判断，得出结论，因为我们通常情况下不可能了解未知系统的所有信息。

比如，要判断工厂里生产出来的手机的质量是否达标，我们不可能去把每一手机都进行检查；要判断一种化肥对农作物的影响，我们也不可能大规模的进行田间试验等等。

这些就是统计学要解决的问题，从学术角度来讲就是根据数据信息对未知的参数做出估计和判断，即统计学重要内容之一——统计推断。

首先，我们从数据的基础信息说起。

数据信息无外乎就有三种：总体信息、样本信息和先验信息。

总体信息是指所研究事件的分布情况等，如人的身高符合正态分布。

样本信息是从总体抽取的样本给我们提供的信息。

人们希望对这些有限的样本信息加以分析和处理得出关于总体的一些特征和信息。

至此，我们引出统计学中重要的一派——频率派。

频率派认为样本信息来自总体，仅通过研究样本信息可以对总体信息做出合理的推断和估计，并且样本越多，就越准确。

说起频率派就不得不提统计学领域的大牛罗纳德·费希尔 (Ronald Aylmer Fisher，1890–1962)，现代统计学专业教科书中的很多内容都是来源于这位的研究工作。

费希尔

费希尔毕业于英国剑桥大学，受到过系统的数学和理论物理专业的训练。

他继承了高斯、勒让德、皮尔逊等人的研究成果，充分发挥出了他的数学和理论功底，对实验设计、数据收集等进行了系统的研究和论述，使统计学真正成为了一门较为系统的研究领域。

他发表的《试验设计》、《统计方法和科学推理》构成了医药等行业统计分析的基础。

在剑桥期间，他制造了那个大名鼎鼎的女士品茶案例，那个发生在剑桥的阳关明媚的午后的故事，使统计学充满了童话般浪漫主义的色彩，一本著名的统计史的著作还以此故事命名。

频率派的统计学方法在二十世纪下半叶在农业、医学、经济、管理、军事等领域获得了广泛的应用。

为了更具体的描述频率派的方法，我们举个栗子。

比如我们想了解一个公交站在下一个单位时间内候车的人数情况。

常识告诉我们候车的人数分布应该是符合泊松分布的：

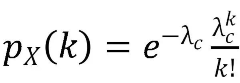
也就是说单位时间内有k个人候车的概率，我们可以通过带入这个公式直接计算出来。

但是，我们面对的问题就是我们虽然知道这个分布公式，但其中有个未知参数λc。

所以，我们需要做的就是在已知分布的情况下如何去估计分布中未知的参数λc。

参数估计的经典方法认为未知参数λc是一个固定的常数，只不过是我们并没有确切的知道这个值。但是我们可以通过抽样得到的数据信息对这个值进行估计。

为此费希尔把高斯的极大似然估计方法做了重新论述，使之用来对参数进行估计。

简要说一下这个方法的大概思路。

我们从车站观察了5次，x1、x2、x3、x4、x5，我们认为在仅有的实验条件下出现的结果应该就是最大概率出现的结果。

所以我们写出似然函数：

然后求使得这个式子达到最大值的λc的值。

由于对数的单调性，通常会取对数再求极值。

具体计算省略掉，得到的值为：

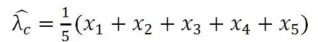
这便是费希尔的经典方法。

可见，频率派基于样本信息便可以得到总体的参数信息，好了，频率派先说到这。

简单说来，就是，先判断总体分布，然后从总体中取样，再通过统计方法进行参数估计。

这不是一个很好的方法吗？看上去一切都很完美，没有任何瑕疵。

也的确如此，在费希尔之后，很多统计学家继承了频率派的研究方法，使这个派的势力日渐壮大，并一度处于江湖中的统治地位。

那贝叶斯派是如何诞生和发展起来的呢？

大家别忘了，还有另外一个信息，我们还没有提及、那就是第三种信息——先验信息，是指在抽样之前基于人们经验或者历史资料得到的一些关于总体的参数信息。

先验信息在我们日常生活当中会自觉或不自觉的使用。

前两种信息，加上第三种信息，进行统计推断，我们成为贝叶斯派。

贝叶斯派起源于英国学者贝叶斯发表的一篇“论有关机遇问题的求解”的文章，不好意思，又是英国人。

在论文中，他提出著名的贝叶斯公式和一种归纳推理方法。

然而，在贝叶斯之后，该方法长久没有得到发展。

直到二次大战之后，人们才愈发感受到贝叶斯方法的巨大潜能，并一举打破经典统计学（频率派）一统天下的局面。

贝叶斯

贝叶斯学派的最基本观点就是：任何一个未知量都可以看作是随机的，应该用一个概率分布去描述未知参数，而不是频率派认为的固定值。

在进行参数估计之前，通过先验信息，我们常常可以得到一个关于未知参数的概率分布，即先验分布，或主观分布。

这在频率派看来是根本不允许的，说好的未知参数是一个固定值，只能通过大量的重复的实验频率来确定，怎么到这里成了一个不确定的值了呢？

一句话而言，频率派认为未知参数是客观的，贝叶斯派认为未知参数可以先从主观角度来考虑。

有没有发现这两个门派的矛盾已经开始显现？

这就像两个不同的世界观，一个说世界是客观的，一个说世界是主观的。

世界观不同，方法论自然就会不同，所以他们两者的不同已经不是技术层面的问题了，而是上升到哲学层面。

好了，先不讨论哲学了，具体根据上边的例子我们说明一下，贝叶斯方法是如何估计λc的。

贝叶斯认为，λc不应该是一个固定值，而应该是一个随机变量。

我们平时根据经验，可以对做出一个分布的估计。

在这个例子中，我们根据平时候车的经验，感觉λc的值有75%的可能是10，有25%的可能是8，基本上没有其他的可能性了。

用贝叶斯方法的描述就是，关于λc的先验分布为：

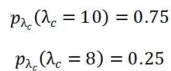
如果我们现在去公交车站，观察了一次，X=7，也就是说我们获得了最新的数据信息。

最新的数据信息有助于我们更新对λc的认识，即更新关于λc的先验分布。

应用贝叶斯定理，得到:

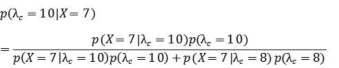
带入

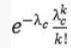
，得到：

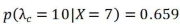
同理得：

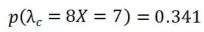
所以，通过我们获得的信息，我们更新了我们对于先验分布的认识，从而得到了后验分布。

从认知的角度而言，贝叶斯方法是一个动态的过程。

随着我们经验的积累、获取数据的积累，对未知参数的估计不断进行着调整。

所以，贝叶斯方法很快在自然语言处理方面展现出了较好的特性。

贝叶斯派的蓬勃发展致使两派斗争如火如荼，无数学者前赴后继。

频率派诟病道：把未知参数看成是随机变量是否妥当？先验分布到底是否存在？如何选取？

贝叶斯学派反击道：频率派中的置信区间能够覆盖到真实参数的概率是1-α，这与未知参数是固定值的观点相互矛盾！

而贝叶斯方法本身就认为未知参数是随机的，不存在这样的问题！

频率派认为很多的估计结果都需要大量的重复的实验去验证。

但是实际操作中，很多情况下是没有条件也不允许这样的重复实验，往往大都是针对某一问题使用一次！

贝格尔（Berger，1985）说：“防止误用的最好方法是给人们在先验信息方面以适当的教育，另外在贝叶斯分析的最后报告中，应将先验分开来写，以便使其他人对主观输入的合理性做出评价。”

Good（1973）更是直截了当的说：“主观主义者直抒他们的判断，而客观主义者以假设来掩盖其判断，并以此享受科学客观性的荣耀。”

关于这两派的争论还将继续下去，相信也不会分出胜负，对于我们这些吃瓜群众而言，争论足够精彩就足矣！

何况两大门派现在都在人工智能和机器学习领域扮演者重要的角色，给我们的生活带来着这样那样的惊喜！

本文作者：伊随，中国科学技术大学，计算机专业博士，主要研究兴趣是人工智能和大数据。