本文转自 CSDN

最近看了篇Paper（Hyperspectral Image Classification Through Bilayer Graph-Based Learning），里面出现了一个超图（Hypergraph）的概念，在这里对它的概念进行说明。

超图（Hypergraph）是什么

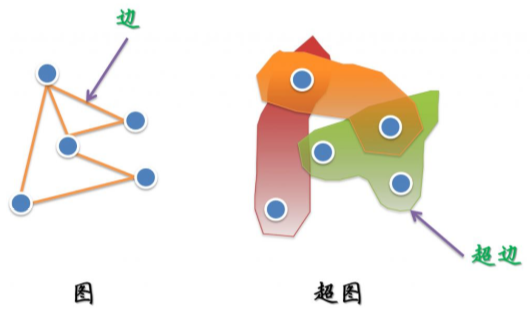
简单的来说，对于我们熟悉的图而言，它的一个边（edge）只能和两个顶点连接；而对于超图来讲，人们定义它的边（这里叫超边，hyperedge）可以和任意个数的顶点连接。一个图和超图的示意图如下所示：

而对于超图的一个严格的数学定义，维基百科上是这样写的：

在数学中，超图是图的一般化。对于超图来说，它的一条边可以连接任意数量的顶点。正式的说，超图H可以表示为H=(X,E)，X为元素的集合，成为节点或顶点，E是X的一组非空子集，成为超边。（In mathematics, a hypergraph is a generalization of a graph, where an edge can connect any number of vertices. Formally, a hypergraph H is a pair H = (X,E) where X is a set of elements, called nodes or vertices, and E is a set of non-empty subsets of X called hyperedges or links.）

超图划分介绍

超图划分的目的在于，将超图的节点划分为 k 个大致相等的部分，且出现同一个超图连接多个部分的节点的情况被最小化。

超图划分的用处范围很广，比如在数据存储中如何减少存取操作将大大影响其工作效率，通过超图能够将关联紧密的数据划分在一起。如此，每次存取操作都按一个部分来进行，将能够有效的减少存取操作的次数。

METIS(普通图的划分算法)

多层图形划分算法，它可以最优的找出图形的对等分，并且速度要快于迄今最优秀的基于光谱的对等方算法( the hitherto state-of-the-art spectral-based bisection techniques )两个数量级。

METIS 只适用于普通图而不是用于超图，所以有一种方案是直接将超图转化为普通图，即用一个团来表示一条超边。

显然这样的方案是有着缺陷的，普通图中的团无法

另外一种方案是直接对超图进行粗化和细化。

hMETIS(超图的划分算法)

hMETIS程序下载地址: http://glaros.dtc.umn.edu/gkhome/metis/hmetis/overview

k-均匀超图（k-uniform hypergraph）

对于超图而言，还有一个k-均匀超图的概念（k-uniform hypergraph）。它指超图的每个边连接的顶点个数都是相同的，即为个数k。所以2-均匀超图就是我们传统意义上的图，3-均匀超图就是一个三元组的集合，以此类推。

While graph edges are pairs of nodes, hyperedges are arbitrary sets of nodes, and can therefore contain an arbitrary number of nodes. However, it is often useful to study hypergraphs where all hyperedges have the same cardinality: a k-uniform hypergraph is a hypergraph such that all its hyperedges have size k. (In other words, it is a collection of sets of size k.) So a 2-uniform hypergraph is a graph, a 3-uniform hypergraph is a collection of triples, and so on.