转自 果壳网
前言:海盗其实是世界上最民主的团体,参加海盗的都是桀骜不驯的汉子,富有独立精神。关于海盗,你一定听说过来自《科学美国人》上著名的“海盗分金”问题。对于这个问题,死理性派不仅可以给出解答,还做出了更深层的推广。
海盗分金是一个非常古老的问题,在1999年《科学美国人》正式把它发表之前,已经至少流行10年了,相信很多人都有所耳闻,也知道解法。此前死理性派也对这个问题也有所 涉及 。今天我们就来回顾一下这个有意思的问题,并且在把问题推广到大规模海盗团伙后,会得出一些非常有意思的结论。
分金的规则
有五个非常聪明的海盗,他们都是死理性派,编号分别是P1、P2、P3、P4、P5。他们一同抢夺了100个金币,现在需要想办法分配这些金币。
海盗们有严格的等级制度:P1
海盗们的分配原则是:等级最高的海盗提出一种分配方案。然后所有的海盗投票决定是否接受分配,包括提议人。并且在票数相同的情况下,提议人有决定权。如果提议通过,那么海盗们按照提议分配金币。如果没有通过,那么提议人将被扔出船外,由下一个最高等级的海盗再提出新的分配方案。
海盗们基于三个因素来做决定。首先,要能留在船上存活下来。其次,要使自己的利益最大化(即得到最多的金币)。最后,在所有其他条件相同的情况下,优先选择把别人扔出船外(这是因为每个海盗都想夺占这条船的控制权)。
海盗的逻辑
现在,假如你是等级最高的P5,你会做何选择?直觉上,为了保住自己的生命,你可能会选择留给自己很少的金币,以便让大家同意自己的决策。然而,结果和此大相径庭。
解决这个问题的关键在于换个思维方向。与其苦思冥想你要做什么决策,不如先想想最后剩下的人会做什么决策。假设现在只剩下P1和P2了,P2会做什么决策?很明显,他将把100金币留给自己,然后投自己一票。由于在票数相同的情况下提议人有决定权,无论P1同不同意,P2都能毫无危险地将所有金币收入囊中。
现在再把P3考虑进来。P1知道,如果P3被扔下海,那么游戏就会出现上述的情况,自己终将一无所获。由于他们都很聪明,P3同样能看到这一点,所以他知道,只要给P1一点点利益,P1就会投票支持他的决策。所以P3最终的决策应该是:( P3,P2,P1 ) → ( 99,0,1 )
P4的策略也类似:由于他需要50%的支持率,所以他只需贿赂1个金币给P2就可以了。P2一定会支持他(否则轮到P3做决策,他就一无所获啦)。所以P4最终的决策是:( P4,P3,P2,P1 ) → ( 99,0,1,0 )
P5的情况稍有不同:由于这次一共有5个人,他至少需要贿赂两个海盗才能使自己的决议通过。所以决策就是:( P5,P4,P3,P2,P1 ) → ( 98,0,1,0,1 )
这个结果是不是很出乎意料?你不但可以保全自己,还能得到绝大部分的利益!其实这里面蕴含着递归的思想,它是解决许多问题(如汉诺塔问题,全排列问题,整数划分问题等)的有利手段。好了,看到这里,想必你一定在感慨:哎,还是做上司(等级高)好啊!且慢!问题还没有结束。
如果有更多的海盗
真实情况下海盗的数目肯定不止5个。继续按照这个逻辑推理,P6的决策将是:( P6,P5,P4,P3,P2,P1 ) → ( 98,0,1,0,1,0 )
一直到P200,它会给自己留1个金币,同时给剩下所有偶数编号的海盗1个金币。
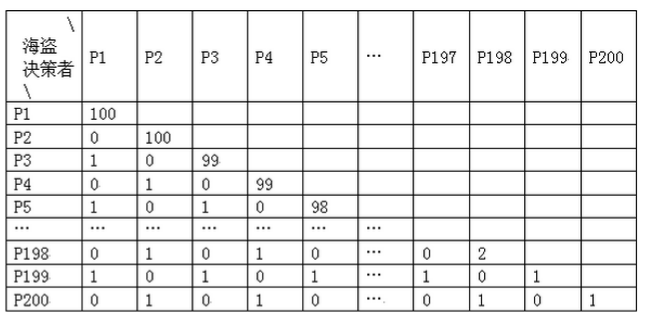
如果海盗数是201个,那么P201该怎么做呢?他好像没有足够的钱去贿赂别的海盗了。不过,为了保住自己的性命,他可以把自己手中的金币全分出去,即给每个奇数编号的海盗(P1~P199)一个金币。这样虽然空手而归,但不至于人财两空。
如果海盗数是202个,P202也只能把这100个金币全部贿赂给其他100个海盗,而这100个海盗必须是在P201做决策时什么也得不到的海盗。由于符合这样条件的海盗有101个(所有偶数编号的海盗+P201),P202的决策不再是唯一的!有101种方案供他选择。
可怜的是P203,由于人数众多,他实在没有足够的钱去贿赂其他海盗以获得足够的支持(他至少还需要获得101个人的支持,但只有100个金币)。所以,不论P203做什么决策,他都难逃被扔出船外的厄运了。不过P203并没有我们想象中的那么悲剧,除非船上正好有且只有203个海盗。不妨再来看增加一个海盗P204的情况。P204明白,P203现在的唯一愿望就是活下来…不论他做什么决策,P203都会举双手支持他(当然举多少手都只能算一票)。所以P204可以靠他自己的一票,P203的一票和贿赂另外100个海盗获得正好50%的支持。
P204可能的决策也只有101种,如下表:(可能获得1金币的海盗用'Y'标示)

P205就没有那么幸运了。他不能无偿的得到P203和P204的支持。所以如果轮到P205做决策,他也必定被扔到船外。P206也一样,尽管他能得到P205的免费支持,但是这还不够。P207需要得到至少104个海盗的支持,所以有了P205,P206的无偿支持还是不够。
P208就比较幸运了,他需要得到104个海盗的支持, P205,P206,P207为了保命会无偿支持他,加上他自己,再贿赂100个海盗,正好104票。
P208可能的决策:

到这里我们又看出了新的规律:
从P201之后,在每两个能够作出决策保住自己生命的海盗之间,存在着一些无论如何决策都会被扔到船外的海盗。而这些海盗会支持在这之后的那个能够做出决策的海盗以保命。用数学来表达,设在P201之后,能在轮到自己作决策时,保住性命的海盗编号所组成的序列为a(n)。我们有
a(0)=202 (1)
a(n)-a(n-1)+100= [a(n)/2] (2)
对于(2),
若a(n)是偶数,则a(n)=2a(n-1)-200
若a(n)是奇数,则a(n)=2a(n-1)-199
给定一个固定的初值,数列的下一项有两个可能解:一个奇数解、一个偶数解,且偶数解比奇数解小1。再考虑我们原问题的意义,当达到偶数解时,偶数编号的海盗已经能够做出决策保全自己。这说明我们应该舍弃所有奇数解(因为相同情况下,海盗会选择把决策人扔出船外)。
由a(n)=2a(n-1)-200以及a(0)=202,得到通解:a(n)=200+ 2 n+1 。考虑到P201也能保全自己,所以我们把所有能够保全自己但却得不到金币的海盗的编号写成统一表达式:
N=200+ 2 n ( n=0,1,2,… )
不难推出这些海盗可能的决策数是在M中任选100的组合数 ,其中
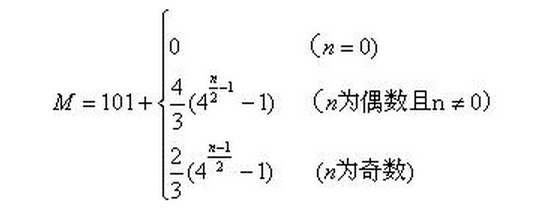
如果我们都是海盗
好了,我们的海盗分金问题就讨论到这里。如果我们把这个模型推广到真实社会里,看看会产生什么结论吧:
你看,其实做上司的风险还是蛮大的。当下属多起来时,自己不但得不到什么好处,甚至连位置都可能保不住。这个简单的模型中也反映出这样一个事实:在一个阶级社会中,人口越少越可能出现独裁。当人口增多而资源紧缺时,如果领导者不能满足大多数人的利益需求,那他的地位也就不稳了。从另外一个角度看,做一个平民还是不错的,不但有机会拿到那一个小小的金币,还不用担心自己被扔出船外,从而可以安心得坐在电脑前,逛逛果壳网,研究研究数学问题。


 技术讨论
技术讨论