本文转自 文克玲科学网博客

今天的数学家都公认，集合论是现代数学的基础。集合论的创始人是德国数学家康托尔。

格奥尔格·费迪南德·路德维希·菲利普·康托尔

格奥尔格·费迪南德·路德维希·菲利普·康托尔于1845年出生在俄国的圣彼得堡，他是个犹太人，但是他们全家都是基督徒，这可能也是后来康托尔性格有些分裂的原因。康托尔12岁的时候，他们全家搬去了德国，到他15岁的时候，他的数学天赋已经显露了出来，他想成为一个数学家，但是他的父亲强迫他学习工程。康托尔不像黎曼那样去跟自己的父亲据理力争，而他的父亲也不像黎曼的父亲那样善解人意，康托尔只是顺从地按照父亲选的道路去前进。这又是康托尔性格中软弱的地方，他总是对自己很不自信，总是希望通过自己的改变来取悦别人。所以后来克罗内克恶毒攻击他的集合论的时候，康托尔不是想办法去争锋相对，而是开始怀疑自己的价值。这也是造成他后来精神分裂的原因之一。

康托尔的父亲后来认识到了自己的错误，所以当康托尔17岁中学毕业时，还是同意了他去学习数学。他先是来到苏黎世大学学习，第二年由于他父亲的去世，他又转学去了柏林大学，专攻数学、哲学和物理，只不过康托尔只对数学和哲学有兴趣，而对物理完全无爱。康托尔在柏林大学时的数学指导老师包括库默尔、魏尔斯特拉斯和以后一生的敌人克罗内克（不知道为什么，很多小个子的人攻击性总是特别强，可能是因为从小由于个子小而产生的不安全感造成的，克罗内克就是个怼天怼地的人）。柏林大学当时由于库默尔、克罗内克的存在，所以算术气氛很浓厚。康托尔在大学期间就钻研了高斯的七封印之书《算术研究》，并以此写出了他的博士论文，在文中他讨论了高斯留下的关于不定方程ax^2+by^2+cz^2=0的x,y,z整数解的难点，并以此论文获得了博士学位。

康托尔像黎曼一样，在博士毕业两年后进入哈雷大学当了一名没有薪俸的老师，1872年他被任命为讲师，到了1879年又被任命为教授。康托尔从一开始就受威尔斯特拉斯的影响，从三角级数理论--特别是傅里叶级数--进入到了数论分析中去。这个理论由于无穷级数的收敛性问题而变得异常困难，康托尔不得不深入到其中去研究理论背后的哲学基础，这样他就开始了"无穷"这个概念本身的数学和哲学问题的全面的分析和研究，而这也是关于连续、极限和收敛等等问题的基础。1872年他在《数学年鉴》上发表了一篇题为《三角级数中一个定理的推广》的论文，把唯一性的结果推广到允许例外值是某种无穷的集合情形。为了描述这种集合，他首先定义了点集的极限点，然后引进了点集的导集和导集的导集等有关重要概念。这是从唯一性问题的探索向点集论研究的开端，并为点集论奠定了理论基础。康托尔在29岁的时候写出了第一篇关于无穷级数的革命性的论文，在这篇论文中，康托尔第一次建立了"全部代数数集合"这个概念，这在当时的数学界无疑是一个石破天惊的创造，标志着一个全新的东西已经出现了。当时康托尔正在因特拉肯度蜜月，正好戴德金也在那里，他们经常在一起交流，戴德金可以说是康托尔当时唯一一个了解自己学说的数学家了。同年他又构造了实变函数论中著名的"康托尔集",给出测度为零的不可数集的一个例子。他还巧妙地将一条直线上的点与整个平面的点一一对应起来，甚至可以将直线与整个n维空间进行点的一一对应。从1879年到1883年，康托尔写了六篇系列论文，论文总题目是"论无穷线形点流形"，其中第五篇论文后来以单行本出版，单行本的书名《一般集合论基础》。康托尔的信条是："数学在它自身的发展中完全是自由的，对他的概念限制只在于：必须是无矛盾的，并且与由确切定义引进的概念相协调。……数学的本质就在于它的自由。"

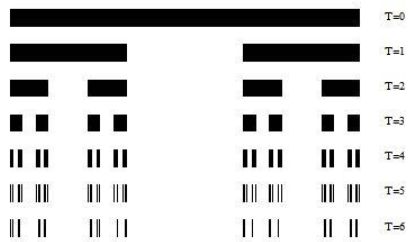
康托尔的构造

康托尔在他的集合论中谈到：实数集合是不可列的。由于实数集合是不可列的，而代数数集合是可列的，于是他得到了必定有超越数存在的结论，而且超越数"大大多于"代数数。这就引发了另外一个概念"超穷数理论"。在他的单行本《一般集合论基础》中的主要成果就是引入了超穷数概念。在书中，康托尔还给出了良序集和无穷良序集编号的概念，指出整个超穷数的集合是良序的，而且任何无穷良序集，都存在唯一的一个第二数类中的数作为表示它的顺序特性的编号。康托尔还借助良序集定义了超穷数的加法、乘法及其逆运算。

集合论基础

康托尔的理论是自芝诺以来人类第一次给"无穷"建立起抽象的形式符号系统和确定的运算，它从本质上揭示了无穷的特性，使无穷的概念发生了一次革命性的变化，并渗透到所有的数学分支，从根本上改造了数学的结构，促进了数学的其他许多新的分支的建立和发展，成为实变函数论、代数拓扑、群论和泛函分析等理论的基础，还给逻辑和哲学带来了深远的影响。

有限个元素的集合的理论是很容易理解的。集合论里，不考虑每个元素的具体性质。两个有限集合的元素数目如果相等，就可以建立元素之间的一一对应关系，因此可以把这两个有限集合定义为等价的。于是，有限集合可以按照元素的数目分类。

自然数集，整数集，有理数集，实数集等是无限集合的例子。它们的“大小”，或者说“元素数目”怎么定义和比较？

康托尔提出，应该用一一对应关系作为对无穷集合分类的准则，并用一个术语：基数(cardinal number)，也叫势(cardinality)来标记无穷集合的“大小”。两个无穷集合之间如果能够建立一个一一对应关系，就说这两个集合有“相同数目的元素”/有相同的势/有相同的基数。

于是我们会得到一些奇怪的，“违反常识”的结论，例如：

1. 偶数集合，奇数集合，自然数集合，整数集合，有理数集合....有相同的“元素数目”/基数；

2. 全体实数集合，[0,1]区间内的实数的集合有相同的“元素数目”/基数；

3. 正方形和它的一条边有相同数目的点。

如此等等。

违反了什么常识？违反了“整体大于部分”。在几何原本里，这可是5条公理之一。

无论如何，康托尔的无穷数理论如今已为数学家广泛接受。“最小的”无穷集合，自然数集合的势称作“可数无限”。比自然数集合更大的，[0,1]区间内的实数的集合--“连续统”的“势”的符号是希伯来文的第一个字母“aleph":ℵ。

如果我们承认康托尔的基本假定：用一一对应关系作为对无穷集合分类的准则，那么由此假定经过逻辑推理得出的一切结论也就不能反对。

剩下的一个问题是：康托尔的无穷数理论尽管看上去很美，它适合我们吗？

我们对物理和数学的关系的基本观点是：数学是物理学家的工具。那么，康托尔的无理数理论，是对我们很好用的工具吗？

请留意博主即将发表的物理数学系列。

以下为参考阅读材料，来自网络：

(1) 康托尔和无穷集合论

格奥尔格·康托尔（Georg Cantor，1845-1918）

康托尔是德国数学家，集合论的创始者。1845年3月3日生于圣彼得堡（今苏联列宁格勒），1918年1月6日病逝于哈雷。其父为迁居俄国的丹麦商人。康托尔11岁时移居德国,在德国读中学。1862年17岁时入瑞士苏黎世大学,翌年转入柏林大学,主修数学，从学于E.E.库默尔、K.（T.W.）外尔斯特拉斯和L.克罗内克。1866年曾去格丁根学习一学期。1867年在库默尔指导下以数论方面的论文获博士学位。1869年在哈雷大学通过讲师资格考试，后即在该大学任讲师，1872年任副教授，1879年任教授。

集合论是现代数学的基础，康托尔在研究函数论时产生了探索无穷集和超穷数的兴趣。康托尔肯定了无穷数的存在，并对无穷问题进行了哲学的讨论，最终建立了较完善的集合理论，为现代数学的发展打下了坚实的基础。

大学期间康托尔主修数论，但受外尔斯特拉斯的影响,对数学推导的严格性和数学分析感兴趣。哈雷大学教授H.E.海涅鼓励他研究函数论。他于1870、1871、1872年发表三篇关于三角级数的论文。在1872年的论文中提出了以基本序列（即柯西序列）定义无理数的实数理论，并初步提出以高阶导出集的性质作为对无穷集合的分类准则。函数论研究引起他进一步探索无穷集和超穷序数的兴趣和要求。

1872年康托尔在瑞士结识了J.W.R.戴德金，此后时常往来并通信讨论。1873年他估计，虽然全体正有理数可以和正整数建立一一对应，但全体正实数似乎不能。他在1874年的论文《关于一切实代数数的一个性质》中证明了他的估计，并且指出一切实代数数和正整数可以建立一一对应，这就证明了超越数是存在的而且有无穷多。在这篇论文中，他用一一对应关系作为对无穷集合分类的准则。

在整数和实数两个不同的无穷集合之外，是否还有更大的无穷?从1874年初起,康托尔开始考虑面上的点集和线上的点集有无一一对应。经过三年多的探索，1877 【注：此处原文缺若干字】

说，“我见到了，但我不相信。”这似乎抹煞了维数的区别。论文于1878年发表后引起了很大的怀疑。P.D.G.杜布瓦－雷蒙和克罗内克都反对，而戴德金早在1877年7月就看到,不同维数空间的点可以建立不连续的一一对应关系，而不能有连续的一一对应。此问题直到1910年才由L.E.J.布劳威尔给出证明。

康托尔在1878年这篇论文里已明确提出“势”的概念(又称为基数)并且用“与自身的真子集有一一对应”作为无穷集的特征。

康托尔认为，建立集合论重要的是把数的概念从有穷数扩充到无穷数。他在1879～1884年发表的题为《关于无穷线性点集》论文6篇，其中5篇的内容大部分为点集论，而第5篇很长，此篇论述序关系，提出了良序集、序数及数类的概念。他定义了一个比一个大的超穷序数和超穷基数的无穷序列，并对无穷问题作了不少的哲学讨论。在此文中他还提出了良序定理（每一集合都能被良序），但未给出证明。

在1891年发表的《集合论的一个根本问题》里，他证明了一集合的幂集的基数较原集合的基数大，由此可知，没有包含一切集合的集合。他在1878年论文中曾将连续统假设作为一个估计提出，其后在1883年论文里说即将有一严格证明，但他始终未能给出。

19世纪70年代许多数学家只承认，有穷事物的发展过程是无穷尽的，无穷只是潜在的，是就发展说的。他们不承认已经完成的、客观存在着的无穷整体，例如集合论里的各种超穷集合。康托尔集合论肯定了作为完成整体的实无穷，从而遭到了一些数学家和哲学家的批评与攻击，特别是克罗内克。康托尔曾在1883年的论文和以后的哲学论文里对于无穷问题作了详尽的讨论。另一方面，康托尔创建集合论的工作开始时就得到戴德金、外尔斯特拉斯和D.希尔伯特的鼓励和赞扬。20世纪以来集合论不断发展，已成为数学的基础理论。

他的著作有：《G.康托尔全集》1卷及《康托尔-戴德金通信集》等。

(2) 集合论的创立者康托尔的遭遇

节选自  解恩泽主编 《科学蒙难集》

19世纪末期，数学界出现了一件引人注目的事情。一位名叫康托尔（G.Cantor，1845－1918）的德国数学家提出一种令人费解的古怪理论----集合论。它的内容是如此与常识格格不入，以至于一出世就引起了一场轩然大波。

康托尔的研究成果发表之后，马上遭致当时一些赫赫有名的数学家的激烈攻击。德国数学家克隆尼克（L.Kronecker，1823－1891）是这些人中言辞最激烈、攻击时间最长的一个。他认为，康托尔关于超限数的研究，是一种非常危险的数学疯病。因而他各种用得上提尖刻语言，粗暴地、连续不断地攻击康托尔达十年之久。他甚至在柏林大学的学生面前公开攻击康托尔，这在许多数学家看来是很过分的事情。克隆尼克的影响还使康托尔的学术论文一再延误发表日期。总之，克隆尼克的专横无理令人震惊，他的激烈攻击使康托尔的精神状态受到极大损害。

除了克隆尼克之外，还有一些著名数学家也对集合论发表了反对意见。法国数学家彭加勒（H.Poi-ncare，1854－1912）说：“我个人，而且还不只我一人，认为重要之点在于，切勿引进一些不能用有限个文字去完全定义好的东西”。他把集合论当作一个有趣的“病理学的情形”来谈，并且预测说：“后一代将把（Cantor）集合论当作一种疾病，而人们已经从中恢复过来了”。德国数学家魏尔（C.H.Her-mann Wey1，1885－1955）认为，康托尔关于基数的等级观点是雾上之雾。菲利克斯．克莱因（F.Klein，1849－1925）也不赞成集合论的思想。数学家H．A．施瓦兹原来是康托尔的好友，但他由于反对集合论而同康托尔断交。

在克隆尼克等人的围攻和反对下，康托尔的精神逐渐崩溃了。从1884年春天起，即在他40岁的时候，他患了严重的忧郁症。1918年，他在哈勒大学附属精神病院去世。一位数学家为自己创立的理论付出这样大的代价，这种事情在数学史上还是不多见的。

集合论的创立和康托尔的遭遇，给后人留下的历史教训是很深刻的。它告诫人们，要坚持和发展科学真理，决不能离开实践。科学理论的对象和内容越是抽象，就越需要深深扎根在现实土壤之中。它还告诫人们，当一种新的科学发现或发明出现的时候，不要凭借直观的、常识或以往的经验来下判断，更不要给科学成果施加某种主观的、人为的标准。真理的唯一标准只能是人们的实践。它告诫那些创造科学新成就的人们，要有充分的精神准备听取各种反对意见，承受可能出现的冷遇、嘲讽和打击，克服前进道路上的各种困难。要充分认识到，获得科学发现是艰苦的，使科学发现为人们理解同样的艰苦的，两者都要经历一个奋斗的过程，决不可能一蹴而就。它还告诫那些评价科学新成新的人们，要冷静、客观、全面地看待每一项科学发现或发明，要善意地对待科学新成果发展过程中难免的缺点和弱点。科学工作者要注意科学道德修养，避免再出现克隆尼克那样的事情。像集合论这样的科学成果，在科学发展中应是越来越多的；而像康托尔这样的悲惨遭遇，则是不应该再出现了。