本文转自CSDN论坛 bitcarmanlee的博客 有修改
1.初见泊松分布
Poisson distribution,翻译成中文名为泊松分布、普阿松分布、帕松分布、布瓦松分布、布阿松分布、波以松分布、卜氏分配等,是概率与统计学中一种常见的离散概率分布,常用来描述单位时间内随机时间发生次数的概率分布。
泊松分布的基本描述:泊松分布在对一个时间或空间间隔内事件发生的次数的建模是非常常用的。若随机变量X服从参数为λ的泊松分布,则可以记为X∼π(X),或者X∼P(X)。其中,参数λ是单位时间内随机事件X 发生的平均概率。
2.从二项分布到泊松分布
博主当年上大学的时候,因为学习不是很认真,一直没用弄明白泊松分布这分布还有那分布到底是个什么鬼。这里咱们先给出一个结论:泊松分布是二项分布的极限情况。具体推导过程,且看下面咱们的解释。
先看看咱们最熟悉的二项分布。说到二项分布,自然就以抛硬币为例。假设我们抛4次硬币,P(x)表示有x次硬币正面朝上,二项分布的概率为:
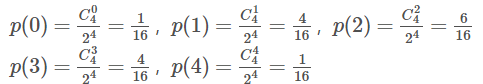
上面的计算也很简单,无需过多解释。不过需要提及的一点是,二项分布中的随机变量X是离散变量,如果是连续变量呢?就该轮到我们的泊松分布登场了。
举一个泊松分布中常用的例子。假设我们现在要估计某个路口一小时经过k辆车的概率。那么第一步,肯定是先大量观察一段时间,获取一小时的时间内通过的汽车数量的期望λ。例如连续三天的14:00-17:00都在路口观察,得到最终的期望值λ。然后我们把每小时分为60min。同时,还假设每分钟的时间间隔内,要么经过一辆车,要么没有车。根据咱们上面的二项分布,很容易得出以下概率:
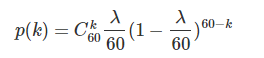
其中,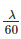 表示每分钟都有一辆车经过的概率。
表示每分钟都有一辆车经过的概率。
很明显,实际情况中,并不是真的每分钟只有一辆车经过,大路口每分钟有很多车经过是很正常的现象。那说明之前的假设不成立,怎么办呢?学过微积分的同学们都知道,很简单,继续分嘛。一分钟的精度如果不够,咱们分成半分钟;半分钟的精度如果还不够,分成一秒钟…..如果这么一直下去取极限,我们就得到了泊松分布,其实也就是二项分布的极限情况!
写到这里为止,先将泊松分布的表达式给出:
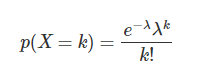
其中λ是单位时间内随机事件的平均发生率。
3.泊松分布的推导
在二项分布的伯努利试验中,如果试验次数n很大,二项分布的概率p很小,且乘积λ= np比较适中,则事件出现的次数的概率可以用泊松分布来逼近。事实上,二项分布可以看作泊松分布在离散时间上的对应物。
证明:
首先回顾e的定义:
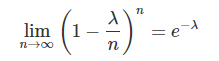
而二项分布的定义:
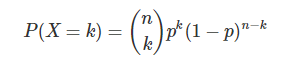
如果令p=λ/n,有:
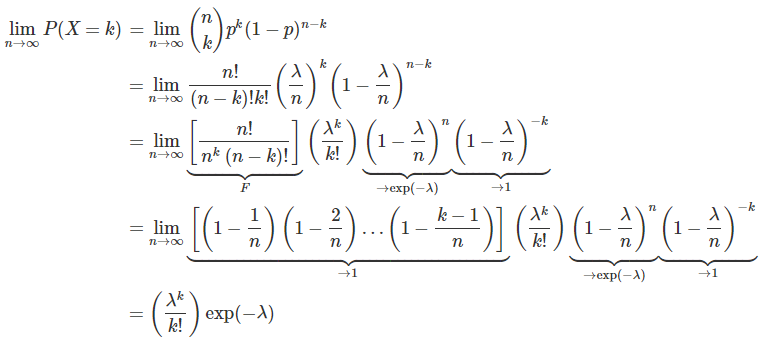
看完上述推导过程以后,想必对泊松分布是二项分布的极限情况这个概念应该有更深入的了解。
此外,泊松分布建模必须满足一下假设:
1、变量k表示的是在一个区间内事件发生的次数,且k能够从0到n取值。
2、事件的发生时相互独立的。
3、事件发生率的常数,也就是说在相同的长度的间隔内,事件平均发生的次数是一样的。
4、某一个瞬间只能发生一个事件。
5、事件发生的概率与区间是成比例的。
6、泊松分布能够由一个二项分布给出。
4.泊松分布的一些属性
泊松分布有两大主要属性——1、泊松分布的期望值和方差都等于lambda;2、满足泊松分布的多个相互独立的随机变量之和仍是满足泊松分布的,lambda为所有泊松分布变量的lambda之和。
泊松分布的属性图如下:
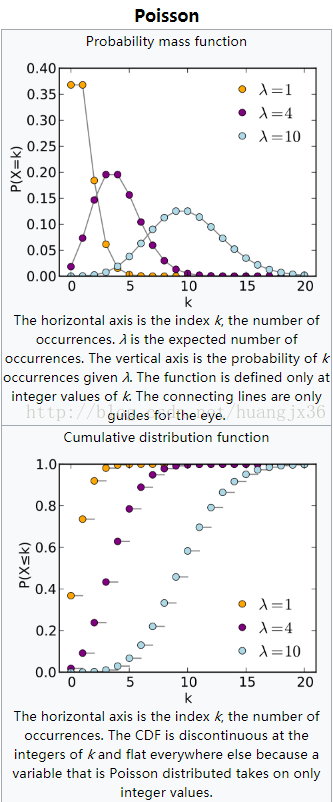
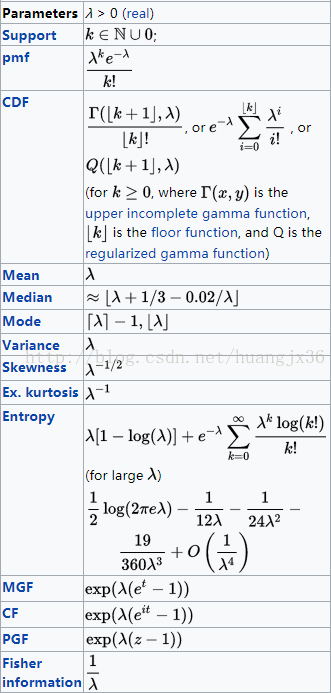
5.再看个实例
如果某个小商店,平均每周卖出两个水果罐头。问:该小商店水果罐头的最佳库存为多少?
假定水果罐头的销量不存在季节性因素,可以近似认为满足下列条件:
1.顾客购买水果罐头是小概率事件。
2.顾客购买水果罐头是独立事件。
3.顾客购买水果罐头的概率是平稳的,不会发生突变。
在统计学上,只要某类事件满足以上三个条件,就可以认为它服从’泊松分布’。
根据前面泊松分布的公式:
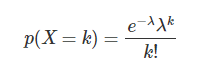
具体到本例中:
P:每周销售k个罐头的概率
X:水果罐头的销售变量
k:X的取值(0,1,2,3…)
λ:每周水果罐头的销量,本例中为2
有泊松分布的公式,可以计算得出每周销售的分布:
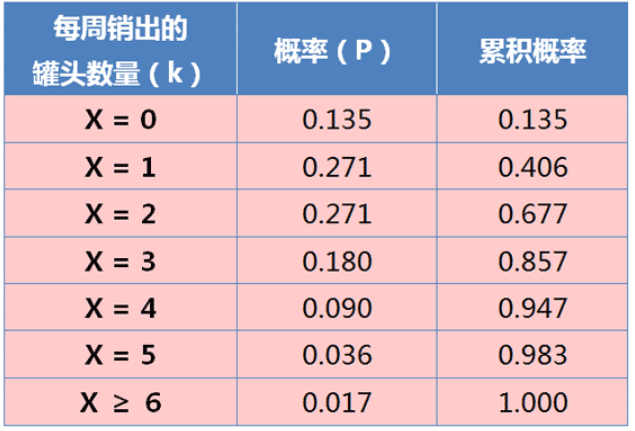
从上表可见,如果存货4个罐头,95%的概率不会缺货(平均每19周发生一次);如果存货5个罐头,98%的概率不会缺货(平均59周发生一次)。
注:罐头的例子来自网络。找不到原始的出处了,所以没有给相应的来源信息。
6.与伽马(gamma)分布的关系
伽马分布是概率统计的万人迷,到处都可以见到他的身影。咱们先看看伽马函数的定义:
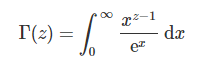
如果z为正整数,那么伽马函数可以定义为:
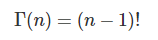
这就显示除了伽马函数与阶乘之间的联系。很明显可以看出,伽马函数将n!的计算扩展到了实数域与复数域。
将上面的伽马函数做个简单处理,可以得到:
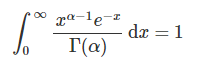
取上式中的函数作为概率密度,可以得到一个最简单的Gamma分布的密度函数:
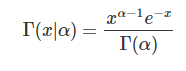
对比一下我们之前的泊松分布:
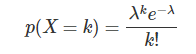
在Gamma分布中,如果令α=k+1,可以发现Gamma分布于泊松分布是完全一致的!
所以,泊松分布于Gamma分布的区别在于,泊松分布是离散的,而Gamma分布是连续的,最直观的解释就是Gamma分布是泊松分布在正实数集上的连续化!
该贴被huang.wang编辑于2018-8-31 12:08:09


 技术讨论
技术讨论