![北京联动北方科技有限公司]()
堆排序与
快速排序,
归并排序一样都是时间复杂度为O(N*logN)的几种常见排序方法。学习堆排序前,先讲解下什么是数据结构中的二叉堆。
二叉堆的定义
二叉堆是完全二叉树或者是近似完全二叉树。
二叉堆满足二个特性:
1.父结点的键值总是大于或等于(小于或等于)任何一个子节点的键值。
2.每个结点的左子树和右子树都是一个二叉堆(都是最大堆或最小堆)。
当父结点的键值总是大于或等于任何一个子节点的键值时为最大堆。当父结点的键值总是小于或等于任何一个子节点的键值时为最小堆。下图展示一个最小堆:
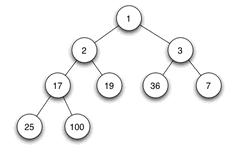
由于其它几种堆(二项式堆,斐波纳契堆等)用的较少,一般将二叉堆就简称为堆。
堆的存储
一般都用数组来表示堆,i结点的父结点下标就为(i – 1) / 2。它的左右子结点下标分别为2 * i + 1和2 * i + 2。如第0个结点左右子结点下标分别为1和2。

堆的操作——插入删除
下面先给出《数据结构C++语言描述》中最小堆的建立插入删除的图解,再给出本人的实现代码,最好是先看明白图后再去看代码。
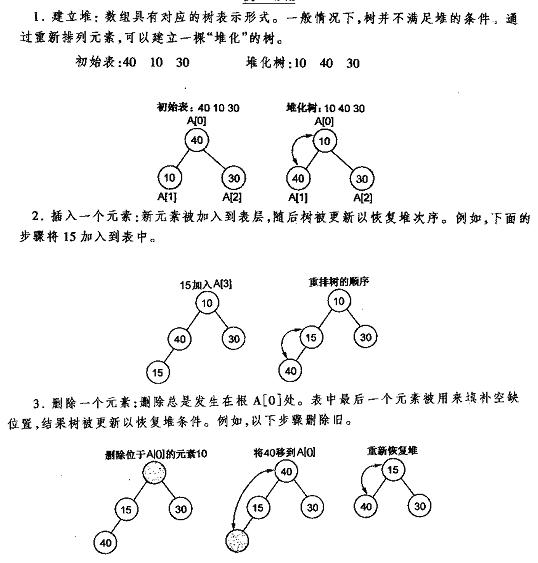
堆的插入
每次插入都是将新数据放在数组最后。可以发现从这个新数据的父结点到根结点必然为一个有序的数列,现在的任务是将这个新数据插入到这个有序数据中——这就类似于直接插入排序中将一个数据并入到有序区间中,对照《白话经典算法系列之二 直接插入排序的三种实现》不难写出插入一个新数据时堆的调整代码:
[cpp]
view plaincopy
- // 新加入i结点 其父结点为(i - 1) / 2
- void MinHeapFixup(int a[], int i)
- {
- int j, temp;
-
- temp = a[i];
- j = (i - 1) / 2; //父结点
- while (j >= 0 && i != 0)
- {
- if (a[j] <= temp)
- break;
-
- a[i] = a[j]; //把较大的子结点往下移动,替换它的子结点
- i = j;
- j = (i - 1) / 2;
- }
- a[i] = temp;
- }
更简短的表达为:
[cpp]
view plaincopy
- void MinHeapFixup(int a[], int i)
- {
- for (int j = (i - 1) / 2; (j >= 0 && i != 0)&& a[i] > a[j]; i = j, j = (i - 1) / 2)
- Swap(a[i], a[j]);
- }
插入时:
[cpp]
view plaincopy
- //在最小堆中加入新的数据nNum
- void MinHeapAddNumber(int a[], int n, int nNum)
- {
- a[n] = nNum;
- MinHeapFixup(a, n);
- }
堆的删除
按定义,堆中每次都只能删除第0个数据。为了便于重建堆,实际的操作是将最后一个数据的值赋给根结点,然后再从根结点开始进行一次从上向下的调整。调整时先在左右儿子结点中找最小的,如果父结点比这个最小的子结点还小说明不需要调整了,反之将父结点和它交换后再考虑后面的结点。相当于从根结点将一个数据的“下沉”过程。下面给出代码:
[cpp]
view plaincopy
- // 从i节点开始调整,n为节点总数 从0开始计算 i节点的子节点为 2*i+1, 2*i+2
- void MinHeapFixdown(int a[], int i, int n)
- {
- int j, temp;
-
- temp = a[i];
- j = 2 * i + 1;
- while (j < n)
- {
- if (j + 1 < n && a[j + 1] < a[j]) //在左右孩子中找最小的
- j++;
-
- if (a[j] >= temp)
- break;
-
- a[i] = a[j]; //把较小的子结点往上移动,替换它的父结点
- i = j;
- j = 2 * i + 1;
- }
- a[i] = temp;
- }
- //在最小堆中删除数
- void MinHeapDeleteNumber(int a[], int n)
- {
- Swap(a[0], a[n - 1]);
- MinHeapFixdown(a, 0, n - 1);
- }
堆化数组
有了堆的插入和删除后,再考虑下如何对一个数据进行堆化操作。要一个一个的从数组中取出数据来建立堆吧,不用!先看一个数组,如下图:
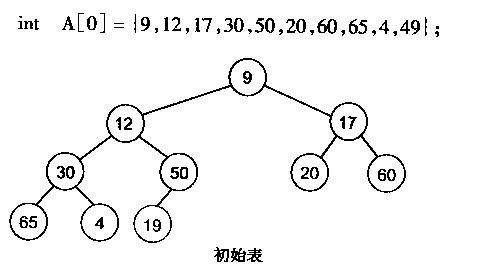
很明显,对叶子结点来说,可以认为它已经是一个合法的堆了即20,60, 65, 4, 49都分别是一个合法的堆。只要从A[4]=50开始向下调整就可以了。然后再取A[3]=30,A[2] = 17,A[1] = 12,A[0] = 9分别作一次向下调整操作就可以了。下图展示了这些步骤:
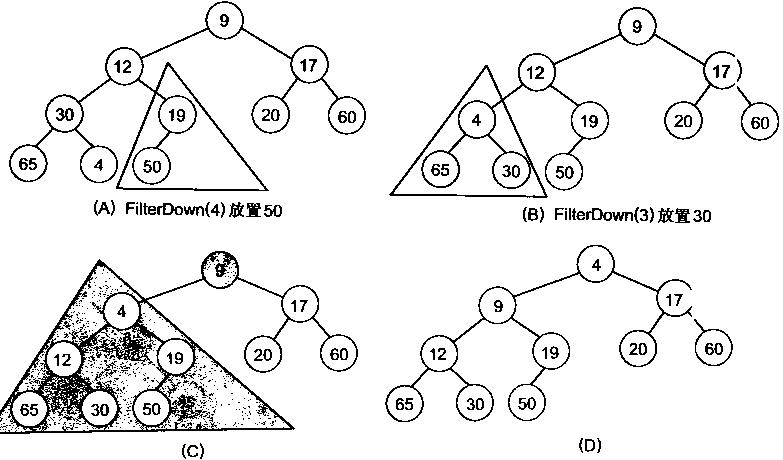
写出堆化数组的代码:
[cpp]
view plaincopy
- //建立最小堆
- void MakeMinHeap(int a[], int n)
- {
- for (int i = n / 2 - 1; i >= 0; i--)
- MinHeapFixdown(a, i, n);
- }
至此,堆的操作就全部完成了(注1),再来看下如何用堆这种数据结构来进行排序。
堆排序
首先可以看到堆建好之后堆中第0个数据是堆中最小的数据。取出这个数据再执行下堆的删除操作。这样堆中第0个数据又是堆中最小的数据,重复上述步骤直至堆中只有一个数据时就直接取出这个数据。
由于堆也是用数组模拟的,故堆化数组后,第一次将A[0]与A[n - 1]交换,再对A[0…n-2]重新恢复堆。第二次将A[0]与A[n – 2]交换,再对A[0…n - 3]重新恢复堆,重复这样的操作直到A[0]与A[1]交换。由于每次都是将最小的数据并入到后面的有序区间,故操作完成后整个数组就有序了。有点类似于直接选择排序。
[cpp]
view plaincopy
- void MinheapsortTodescendarray(int a[], int n)
- {
- for (int i = n - 1; i >= 1; i--)
- {
- Swap(a[i], a[0]);
- MinHeapFixdown(a, 0, i);
- }
- }
注意使用最小堆排序后是递减数组,要得到递增数组,可以使用最大堆。
由于每次重新恢复堆的时间复杂度为O(logN),共N - 1次重新恢复堆操作,再加上前面建立堆时N / 2次向下调整,每次调整时间复杂度也为O(logN)。二次操作时间相加还是O(N * logN)。故堆排序的时间复杂度为O(N * logN)。STL也实现了堆的相关函数,可以参阅《STL系列之四 heap 堆》。
注1 作为一个数据结构,最好用类将其数据和方法封装起来,这样即便于操作,也便于理解。此外,除了堆排序要使用堆,另外还有很多场合可以使用堆来方便和高效的处理数据,以后会一一介绍。


 技术讨论
技术讨论