本文转自 taotao1233
本文的目的是用C实现生成Gabor模版,并对图像卷积。并简单提一下,Gabor滤波器在纹理特征提取上的应用。
一、什么是Gabor函数(以下内容含部分翻译自维基百科)
在图像处理中,Gabor函数是一个用于边缘提取的线性滤波器。Gabor滤波器的频率和方向表达同人类视觉系统类似。研究发现,Gabor滤波器十分适合纹理表达和分离。在空间域中,一个二维Gabor滤波器是一个由正弦平面波调制的高斯核函数。
还有,生物学实验发现,Gabor滤波器可以很好地近似单细胞的感受野函数(光强刺激下的传递函数),什么视皮层内的超柱,bla...bla,总之是这方面仿生的数学模型。
另外,网上有一种说法,gabor分为实部和虚部,用实部进行滤波后图像会平滑;虚部滤波后用来检测边缘。【来自百度知道某个大神的回答】,我查了文献,发现的确有人用Gabor的奇函数部分做边缘提取(《基于Gabor滤波器的边缘检测算法》 无线电工程2000年第3卷第30期)。另外,从我的实验结果也有类似的发现。暂且认为这个对的吧。
Gabor滤波器的脉冲响应,可以定义为一个正弦波(对于二维Gabor滤波器是正弦平面波)乘以高斯函数。由于乘法卷积性质,Gabor滤波器的脉冲响应的傅立叶变换是其调和函数的傅立叶变换和高斯函数傅立叶变换的卷积。该滤波器由实部和虚部组成,二者相互正交。一组不同频率不同方向的Gabor函数数组对于图像特征提取非常有用。
下面给出二维Gabor函数的数学表达:
复数表达:
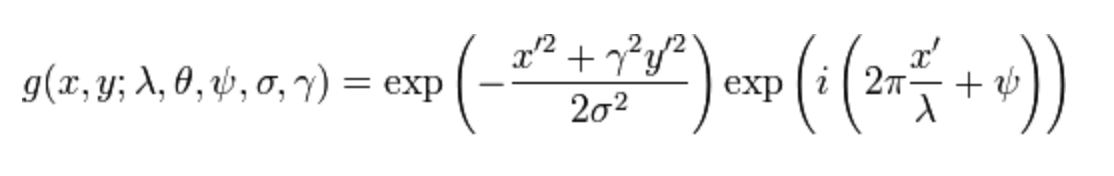
实数部分:
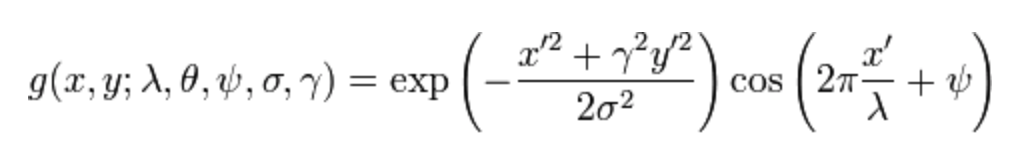
虚数部分:
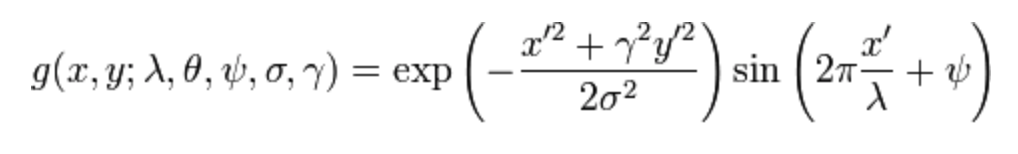
其中:
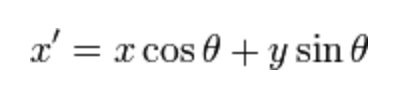
和
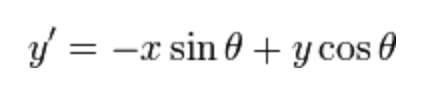
下面介绍公式中各个参数的含义,及参数如何配置问题【都从老外那翻译来的】:
波长(λ):它的值以像素为单位指定,通常大于等于2.但不能大于输入图像尺寸的五分之一。
方向(θ):这个参数指定了Gabor函数并行条纹的方向,它的取值为0到360度
相位偏移(φ):它的取值范围为-180度到180度。其中,0he180度分别对应中心对称的center-on函数和center-off函数,而-90度和90度对应反对称函数。
长宽比(γ):空间纵横比,决定了Gabor函数形状(support,我翻译为形状)的椭圆率(ellipticity)。当γ= 1时,形状是圆的。当γ< 1时,形状随着平行条纹方向而拉长。通常该值为0.5
带宽(b):Gabor滤波器的半响应空间频率带宽b和σ/ λ的比率有关,其中σ表示Gabor函数的高斯因子的标准差,如下:
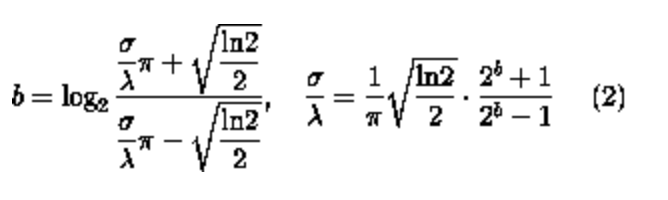
σ的值不能直接设置,它仅随着带宽b变化。带宽值必须是正实数,通常为1,此时,标准差和波长的关系为:σ= 0.56 λ。带宽越小,标准差越大,Gabor形状越大,可见平行兴奋和抑制区条纹数量越多。
下面给出,不同参数配置下的Gabor核函数效果图,大小均100*100:
a.波长对比组【方向为:0,相位偏移量为:0,纵横比率为:0.5,带宽为:1,下图波长分别为5,10,15】

b.方向对比组【波长为:10,相位偏移量为:0,空间纵横比为:0.5,带宽为:1,方向分别为:0,45,90】

c.相位偏移量对比组【波长为:10,方向为:0,空间纵横比:0.5,带宽:1,相位偏移量分别为:0,180,-90,90】

d.空间纵横比对比组【波长:10,相位偏移量:0,方向:0,带宽:1,空间纵横比分别为:0.5,1】

e.带宽对比组【波长:10,方向:0,相位偏移量:0,空间纵横比:0.5,带宽分别为:0.5,1,2】

二、gabor函数实现:
matlab版本,我从pudn上找来的,但他的gabor函数,我没怎么看明白:
gabor函数:
function gabor_k = compute(x,y,f0,theta)
r = 1; g = 1;
x1 = x*cos(theta) + y*sin(theta);
y1 = -x*sin(theta) + y*cos(theta);
gabor_k = f0^2/(pi*r*g)*exp(-(f0^2*x1^2/r^2+f0^2*y1^2/g^2))*exp(i*2*pi*f0*x1);
%绘制一个Gabor滤波器的空域和频域函数图
clear;
x = 0;
theta = 0;
f0 = 0.2;
for i = linspace(-15,15,50)
x = x + 1;
y = 0;
for j = linspace(-15,15,50)
y = y + 1;
z(y,x)=compute(i,j,f0,theta);
end
end
x = linspace(-15,15,50);
y = linspace(-15,15,50);
surf(x,y,real(z))
title('Gabor filter:real component');
xlabel('x');
ylabel('y');
zlabel('z');
figure(2);
surf(x,y,imag(z))
title('Gabor filter:imaginary component');
xlabel('x');
ylabel('y');
zlabel('z');
Z = fft2(z);
u = linspace(-0.5,0.5,50);
v = linspace(-0.5,0.5,50);
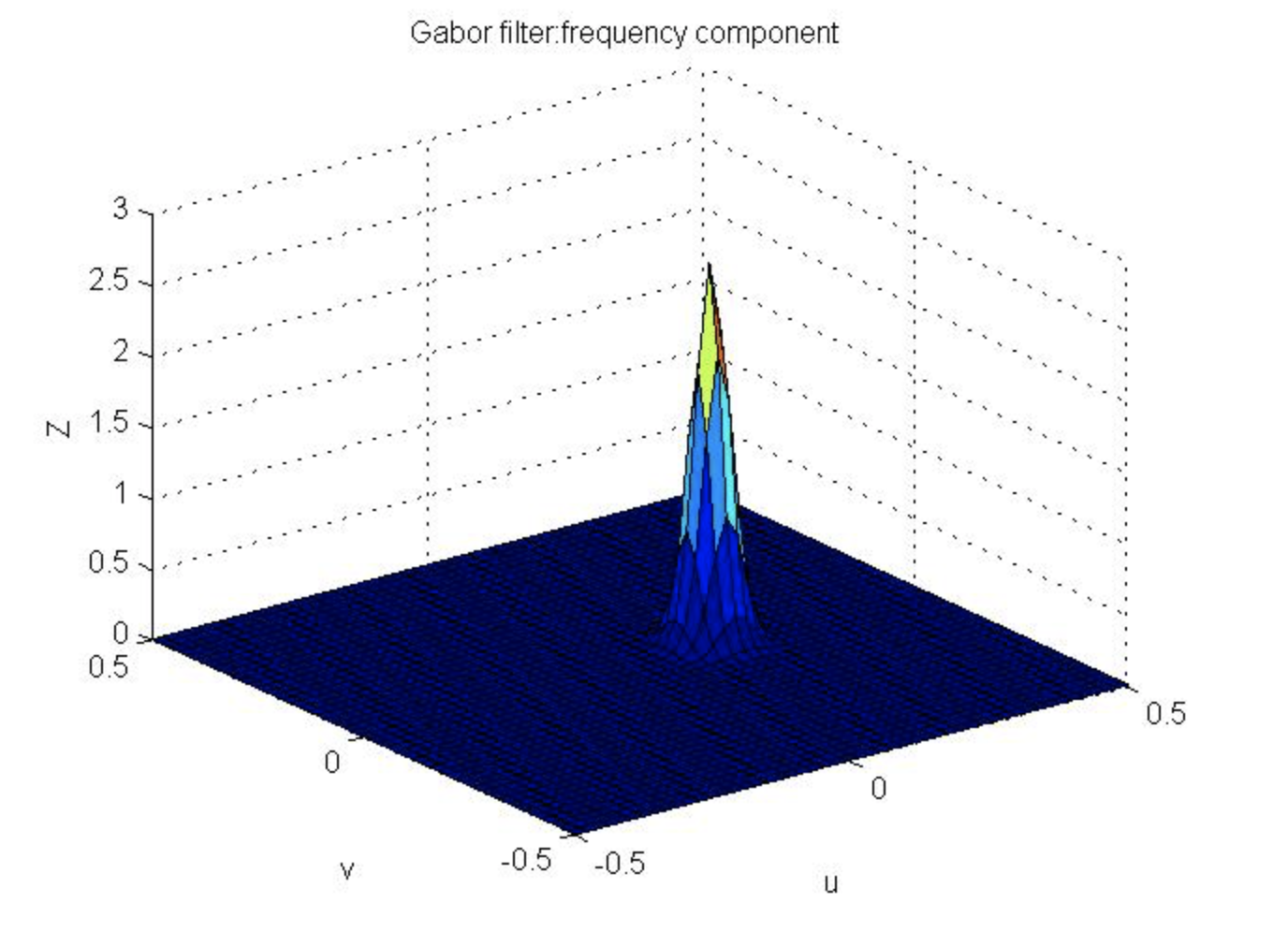
figure(3);
surf(u,v,abs(fftshift(Z)))
title('Gabor filter:frequency component');
xlabel('u');
ylabel('v');
zlabel('Z');
运行结果:
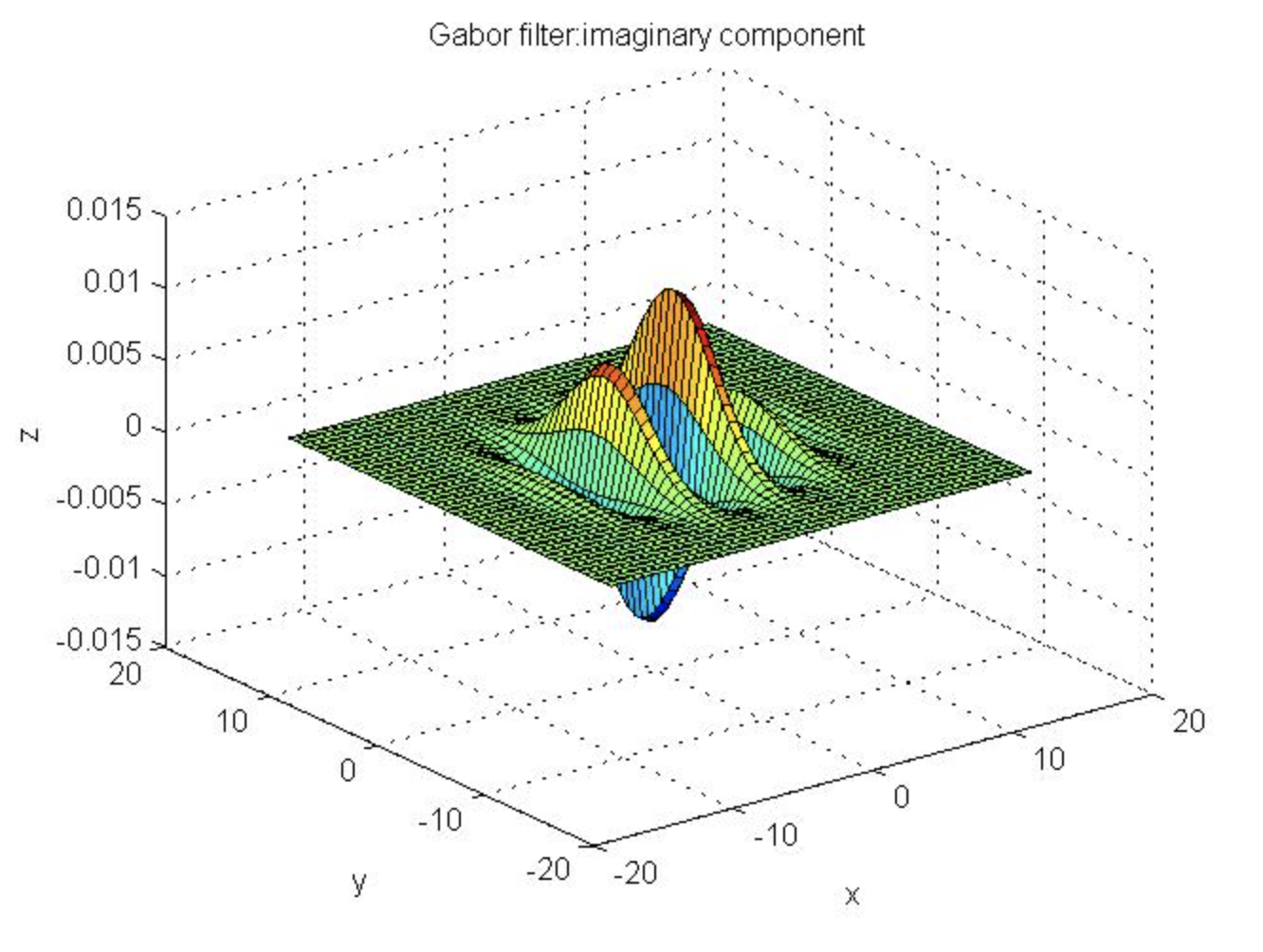
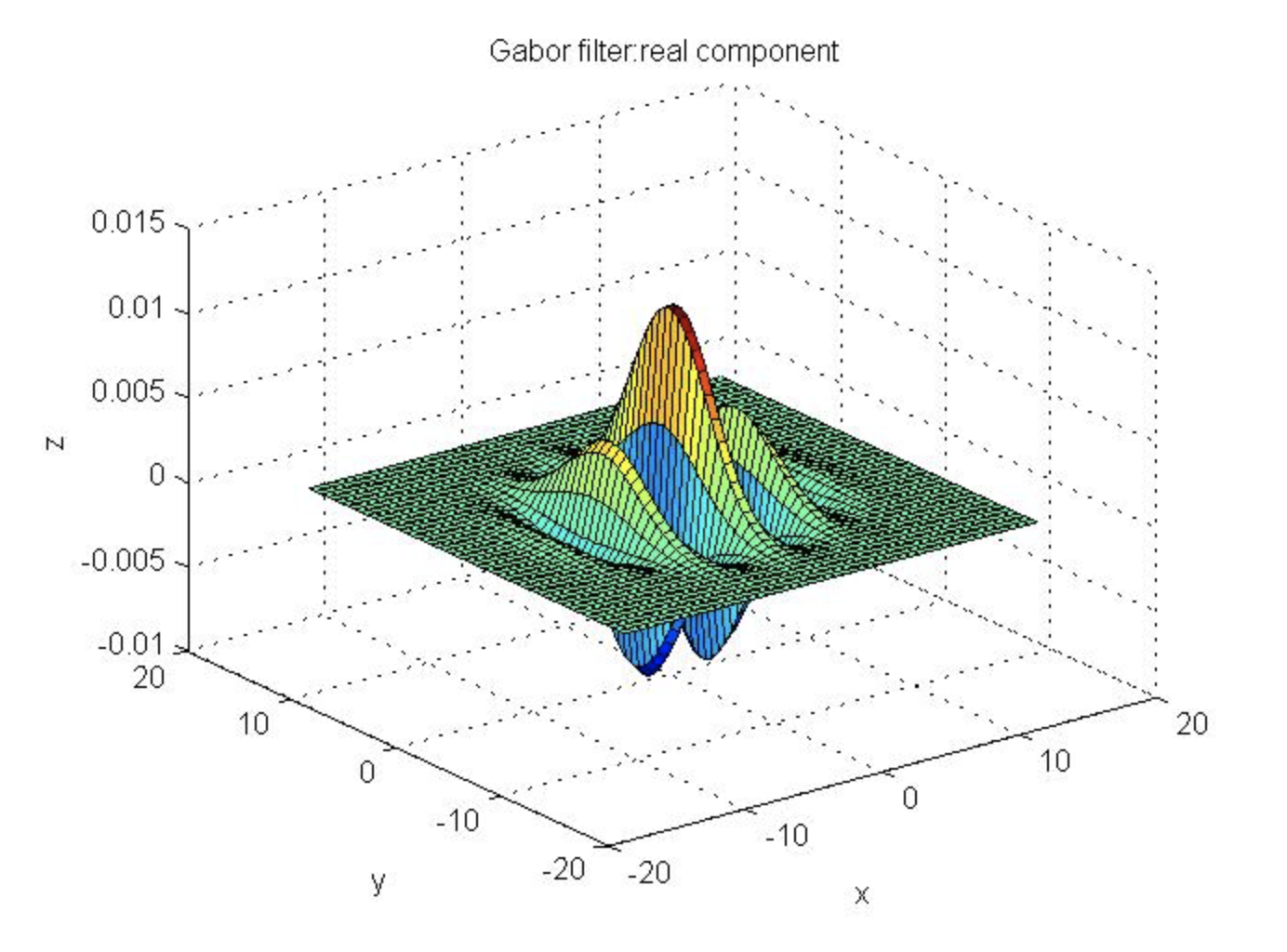
%4个方向的Gabo滤波器通过图像显示
clear;
x = 0;
theta = pi*3/4;%用弧度0,pi/4,pi/2,pi*3/4
f0 = 0.2;
for i = linspace(-15,15,50)
x = x + 1;
y = 0;
for j = linspace(-15,15,50)
y = y + 1;
z(y,x)=compute(i,j,f0,theta);
end
end
z_real = real(z);
m = min(z_real(:));
z_real = z_real+abs(m);
M = max(z_real(:));
imshow(1/M*z_real);
figure(2)
z_imag = imag(z);
m = min(z_imag(:));
z_imag = z_imag+abs(m);
M = max(z_imag(:));
imshow(1/M*z_imag);
运行效果:
实数部分:

虚数部分:

%4个方向的Gabor滤波器对lena进行滤波
clear;
I = imread('.\pic\lena.bmp');
f0 = 0.2;
count = 0;
for theta = [0,pi/4,pi/2,pi*3/4];%用弧度0,pi/4,pi/2,pi*3/4
count = count + 1;
x = 0;
for i = linspace(-8,8,11)
x = x + 1;
y = 0;
for j = linspace(-8,8,11)
y = y + 1;
z(y,x)=compute(i,j,f0,theta);
end
end
figure(count);
filtered = filter2(z,I,'valid');
f = abs(filtered);
imshow(f/max(f(:)))
end
运行效果:
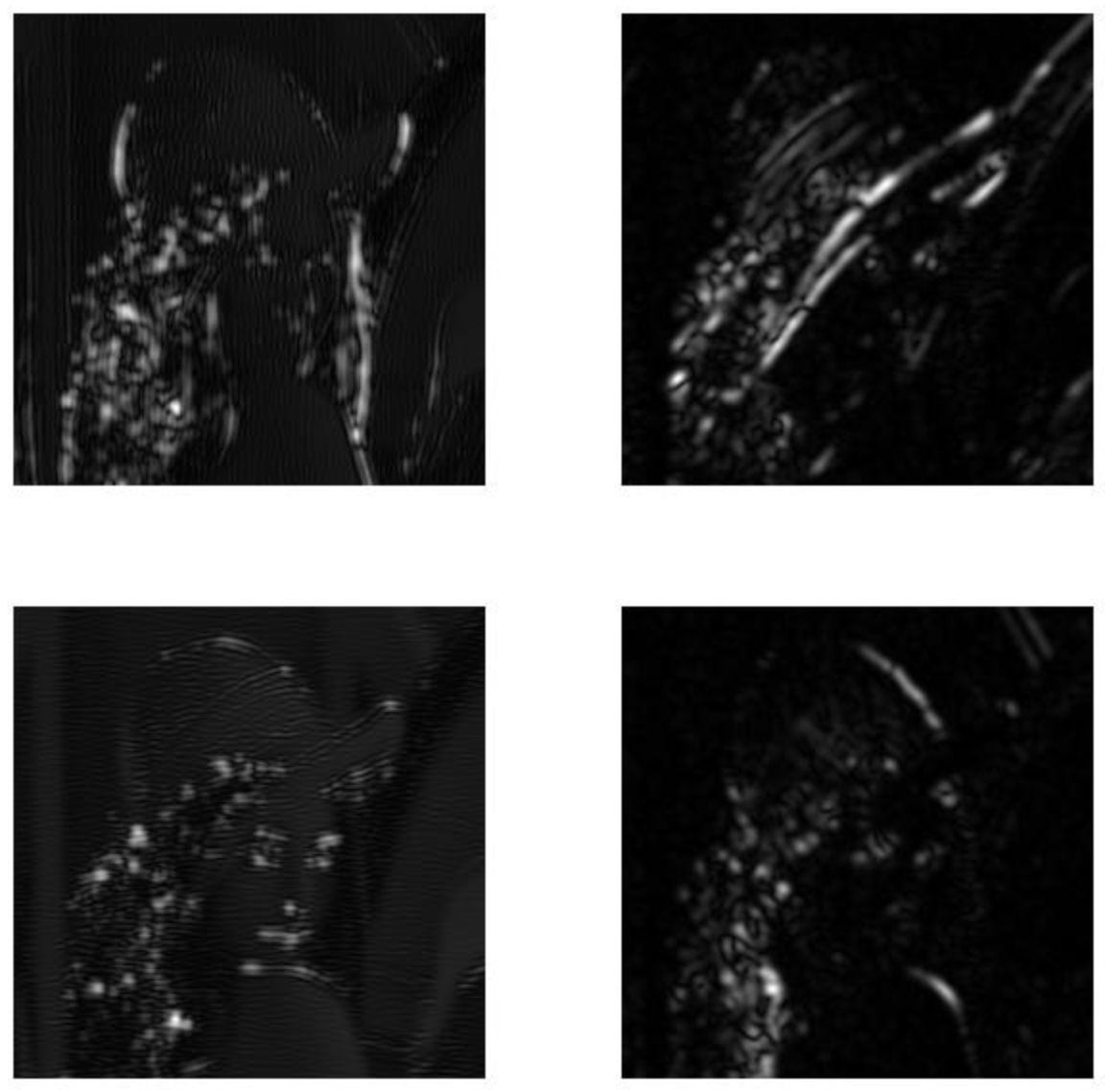
好吧,不管他了。大概感受一下吧。由于我没看明白他的gabor函数怎么定义的,参数设置也不一样,实验结果很不相同,我希望我是对的,天地良心呐!!我只能按照维基百科给出的函数,编写了以下C代码:
// my_gabor.cpp : 定义控制台应用程序的入口点。
//
#include "stdafx.h"
#include<iostream>
#include <opencv2/core/core.hpp>
#include <opencv2/highgui/highgui.hpp>
#include <opencv2/imgproc/imgproc.hpp>
#include "math.h"
#define PI 3.1415926
#define N 4
using namespace std;
using namespace cv;
void m_filer(double *src,int height,int width,double *mask_rel,double *mask_img,int mW,int mH,int k)
{
IplImage *tmp;
double a,b,c;
char res[20]; //保存的图像名称
tmp = cvCreateImage(cvSize(width,height),IPL_DEPTH_8U,1);
for (int i = 0;i < height;i++)
{
for (int j = 0;j < width;j++)
{
a = 0.0;
b = 0.0;
c = 0.0;
//去掉靠近边界的行列,无法滤波,超出范围
if (i > int(mH/2) && i < height - int(mH/2) && j > int(mW) && j < width - int(mW/2))
{
for (int m = 0;m < mH;m++)
{
for(int n = 0;n < mW;n++)
{
//printf("%f\n",src[(i+m-int(mH/2))*width+(j+n-int(mW))]);
a += src[(i+m-int(mH/2))*width+(j+n-int(mW))]*mask_rel[m*mW+n];
b += src[(i+m-int(mH/2))*width+(j+n-int(mW))]*mask_img[m*mW+n];
//printf("%f,%f\n",a,b);
}
}
}
c = sqrt(a*a+b*b);
c /= mW*mH;
tmp->imageData[i*width+j] = (unsigned char)c;
}
}
sprintf(res,"result%d.jpg",k);
cvSaveImage(res,tmp);
cvReleaseImage(&tmp);
}
int _tmain(int argc, _TCHAR* argv[])
{
IplImage *src;
double *rel,*img,*src_data,xtmp,ytmp,tmp1,tmp2,tmp3,re,im;
double Theta,sigma,Gamma,Lambda,Phi; //公式中的5个参数
int gabor_height,gabor_width,x,y;
src = cvLoadImage("test.jpg",CV_LOAD_IMAGE_GRAYSCALE);
gabor_height = 10;
gabor_width = 10;
Gamma = 1.0;
Lambda = 10.0;
sigma = 100;
Phi = 0;
rel = (double *)malloc(sizeof(double)*gabor_width*gabor_height);//实数部分
img = (double *)malloc(sizeof(double)*gabor_width*gabor_height);//虚数部分
src_data = (double *)malloc(sizeof(double)*src->widthStep*src->height); //图像数据
for (int i=0;i<src->height;i++)
{
for (int j=0;j<src->widthStep;j++)
{
src_data[i*src->widthStep+j]=(unsigned char)src->imageData[i*src->widthStep+j];
//printf("%f\n",src_data[i*src->widthStep+j]);
}
}
//构造gabor函数
for (int k = 0;k < N;k++) //定义N方向
{
Theta = PI*((double)k/N);
for (int i = 0;i < gabor_height;i++) //定义模版大小
{
for (int j = 0;j < gabor_width;j++)
{
x = j - gabor_width/2;
y = i - gabor_height/2;
xtmp = (double)x*cos(Theta) + (double)y*sin(Theta);
ytmp = (double)y*cos(Theta) - (double)x*sin(Theta);
tmp1 = exp(-(pow(xtmp,2)+pow(ytmp*Gamma,2))/(2*pow(sigma,2)));
tmp2 = cos(2*PI*xtmp/Lambda + Phi);
tmp3 = sin(2*PI*xtmp/Lambda + Phi);
re = tmp1*tmp2;
im = tmp1*tmp3;
rel[i*gabor_width+j] = re;
img[i*gabor_width+j] = im;
//printf("%f,%f\n",re,im);
}
}
//用不同方向的GABOR函数对图像滤波并保存图片
m_filer(src_data,src->height,src->width,rel,img,10,10,k);
}
free(rel);free(img);free(src_data);
return 0;
}
运行效果:

大概就这样凑活吧。我这边实数部分和虚数部分的处理是采用求模的方式。有问题的,请广大人民群众提出来啊。
三、用gabor提取纹理特征的思路【抄别人的论文】
Gabor滤波方法的主要思想是:不同纹理一般具有不同的中心频率及带宽,根据这些频率和带宽可以设计一组Gabor滤波器对纹理图像进行滤波,每个Gabor滤波器只允许与其频率相对应的纹理顺利通过,而使其他纹理的能量受到抑制,从各滤波器的输出结果中分析和提取纹理特征,用于之后的分类或分割任务。Gabor滤波器提取纹理特征主要包括两个过程:①设计滤波器(例如函数、数目、方向和间隔);②从滤波器的输出结果中提取有效纹理特征集。Gabor滤波器是带通滤波器,它的单位冲激响应函数(Gabor函数)是高斯函数与复指数函的乘积。它是达到时频测不准关系下界的函数,具有最好地兼顾信号在时频域的分辨能力。
实现步骤:
(1)将输入图像分为3×3(9块)和4×4(16块)的图像块;
(2)建立Gabor滤波器组:选择4个尺度,6个方向,这样组成了24个Gabor滤波器;
(3)Gabor滤波器组与每个图像块在空域卷积,每个图像块可以得到24个滤波器输出,这 些输出是图像块大小的图像,如果直接将其作为特征向量,特征空间的维数会很大, 所以需要“浓缩”;
(4)每个图像块经过Gabor滤波器组的24个输出,要“浓缩”(文中提到“average filter responses within the block”我的理解是取灰度均值)为一个24×1的列向量作为该图像 块的纹理特征。查阅相关文献,发现也可以用方差。
利用一幅真实图像,按照文献原文所说,利用4scales*6orientations的Gabor滤波器组进行纹理特征提取,可以有效获得图像纹理信息。其中,单独拿出某组相同scale的结果,展示如下所示。【别人的实验结果,也没给代码,我也没去做】



 技术讨论
技术讨论